Алгебра, вопрос задал laninaa932 , 1 год назад

За правильный ответ дам 100 баллов Главный мозг помогите пожалуйста с номерами 5,6,8,9

Приложения:

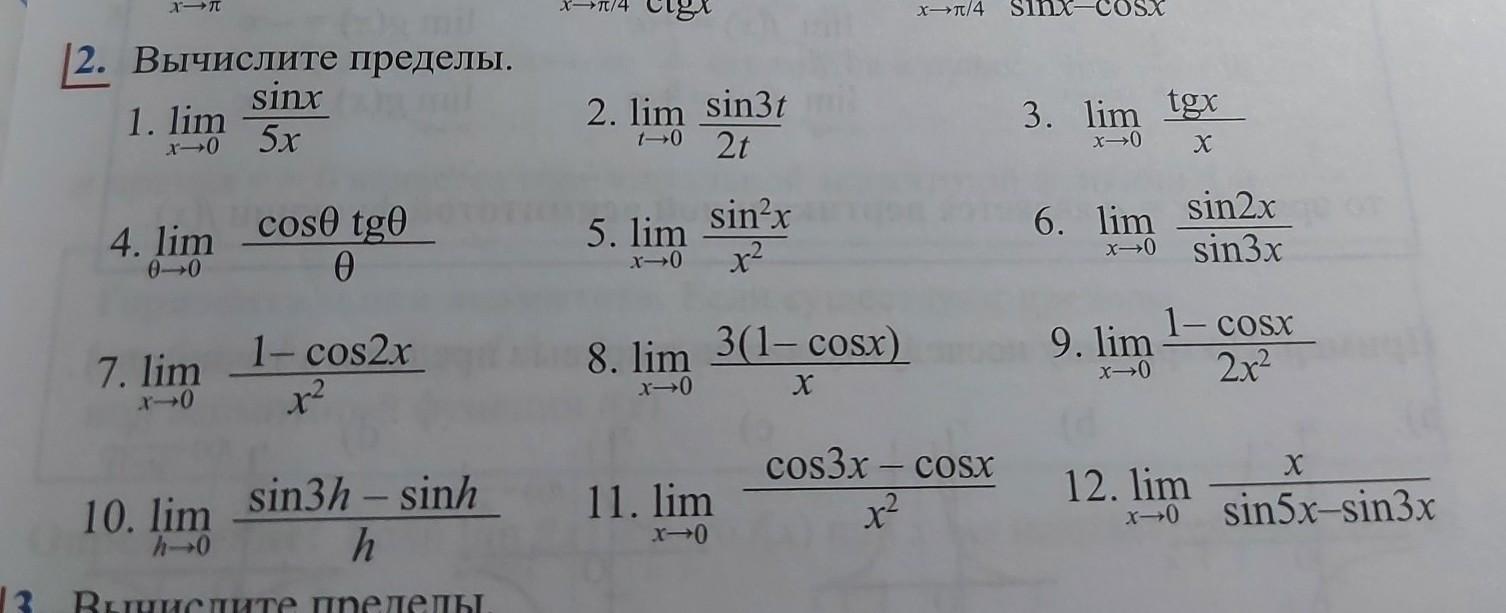
Ответы на вопрос

Ответил NNNLLL54

Ответ:

Применяем 1 замечательный предел : $\bf \lim\limits_{x \to 0}\ \dfrac{sinx}{x}=1$ и формулу

"трёх двоечек" : $\bf sin^2a=\dfrac{1-cos2a}{2}$ .

$\bf 5)\ \ \lim\limits_{x \to 0}\ \dfrac{sin^2x}{x^2}=\lim\limits_{x \to 0}\Big( \dfrac{sinx}{x}\cdot \dfrac{sinx}{x}\Big)=\lim\limits_{x \to 0}\ \dfrac{sinx}{x}\cdot \lim\limits_{x \to 0}\ \dfrac{sinx}{x}=1\cdot 1=1$

$\bf 6)\ \ \lim\limits_{x \to 0}\ \dfrac{sin2x}{sin3x}=\lim\limits_{x \to 0}\Big( \dfrac{sin2x}{2x}\cdot \dfrac{3x}{sin3x}\cdot \dfrac{2}{3}\Big)=\\\\\\=\dfrac{2}{3}\lim\limits_{x \to 0}\ \dfrac{sin2x}{2x}\cdot \lim\limits_{x \to 0}\dfrac{3x}{sin3x}=\dfrac{2}{3}\cdot 1\cdot 1=\dfrac{2}{3}$

$\bf 8)\ \ \lim\limits_{x \to 0}\ \dfrac{3(1-cosx)}{x}=\lim\limits_{x \to 0}\ \dfrac{3\cdot 2sin^2\frac{x}{2}}{x}=6\lim\limits_{x \to 0}\ \dfrac{sin\frac{x}{2}\cdot sin\frac{x}{2}}{(\frac{x}{2})\cdot 2}=\\\\\\=6\lim\limits_{x \to 0}\ \dfrac{sin\frac{x}{2}}{\frac{x}{2}}\cdot \lim\limits_{x \to 0}\ \dfrac{sin\frac{x}{2}}{2}=6\cdot 1\cdot \dfrac{0}{2}=0$

$\bf 9)\ \ \lim\limits_{x \to 0}\ \dfrac{1-cosx}{2x^2}=\lim\limits_{x \to 0}\ \dfrac{2sin^2\frac{x}{2}}{2x^2}=\lim\limits_{x \to 0}\ \dfrac{sin\frac{x}{2}\cdot sin\frac{x}{2}}{\frac{x}{2}\cdot \frac{x}{2}\cdot 4}=\\\\\\=\dfrac{1}{4}\lim\limits_{x \to 0}\ \dfrac{sin\frac{x}{2}}{\frac{x}{2}}\cdot \lim\limits_{x \to 0}\ \dfrac{sin\frac{x}{2}}{\frac{x}{2}}=\dfrac{1}{4}\cdot 1\cdot 1=\dfrac{1}{4}$