за одно задание даю 100 баллов срочно полное оформление
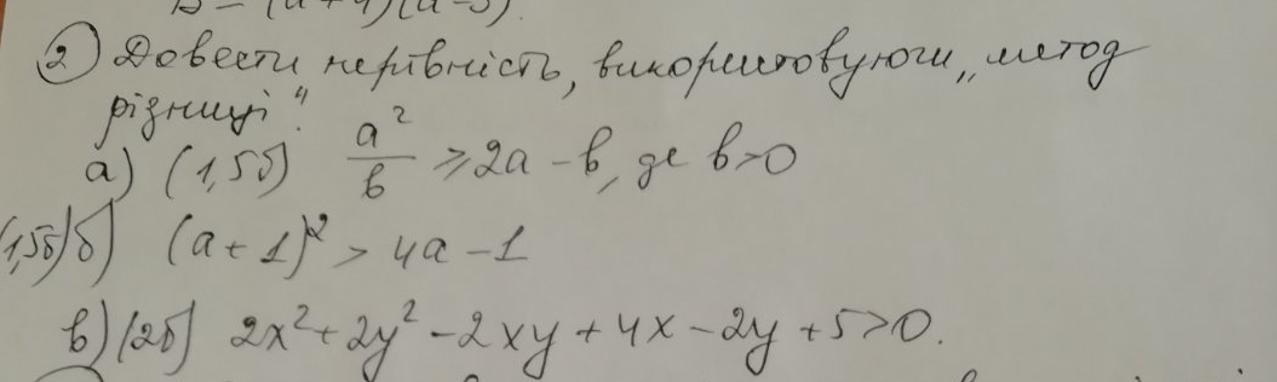
Ответы на вопрос
Ответ:
Неравенства доказаны.
Объяснение:
Доказать неравенства, используя "метод разницы":
- Метод разницы
- Этот метод заключается в том, чтобы рассмотреть разницу между левой и правой частями неравенства и доказать, что это различие принимает значения постоянного знака при любых значениях переменных.
а)
- Любое число в квадрате неотрицательно.
(a - b) ≥ 0; b > 0 ⇒ при любых значениях переменных.
б) (a + 1)² > 4a - 1
(a + 1)² - (4a - 1) > 0
a² + 2a + 1 - 4a + 1 > 0
a² - 2a + 1 + 1 > 0
(a - 1)² + 1 > 0
(a - 1)² ≥ 0 ⇒ (a - 1)² + 1 > 0 при любых значениях переменной.
в) 2x² + 2y² - 2xy + 4x - 2y + 5 > 0
Перепишем выражение в следующем виде и сгруппируем одночлены так, чтобы получились формулы квадратов суммы или разности двух чисел:
x² + x² + y² + y² - 2xy + 4x - 2y + 1 + 4 > 0
(x² - 2xy + y²) + (x² + 4x + 4) + (y² -2y + 1) > 0
(x - y)² + (x + 2)² + (y - 1)² > 0
Данное выражение может быть равно нулю, если все три слагаемые равны нулю одновременно.
Вторая и третья скобки могут быть равны нулю при х = -2 и у = 1.
Тогда значение в первой скобке будет равно:
(-2 - 1)² = 9
То есть наше выражение будет положительно.
Если первая скобка равна нулю, то х = у, тогда сумма второй и третьей скобки будет положительна.
⇒ (x - y)² + (x + 2)² + (y - 1)² > 0 при любых значениях переменных.
Неравенства доказаны.
#SPJ1