За графіком функції у = х² (мал.додаю) опишіть її властивості: яка область визначення цієї функції; на яких проміжках вона зростає; на яких спадає; при якому значенні х функція має найменше значення; чи має вона найбільше значення; чи є дана функція парною або непарною.
Ответы на вопрос
Ответ:
Пошаговое объяснение:
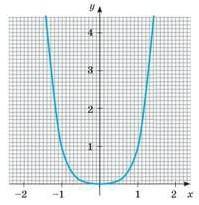
Графік функції y = x² — це парабола, яка відкривається вгору, що означає, що вона має точку мінімуму (глобальний мінімум), і значення y зростають зі збільшенням x.
Областю визначення цієї функції є всі дійсні числа, оскільки функція може бути визначена для будь-якого дійсного значення x.
Функція необмежено зростає зі збільшенням x, що означає, що для значень y немає верхніх меж. Однак функція також падає нескінченно, коли x зменшується, що означає, що для значень y також немає нижніх меж. Іншими словами, функція не має асимптот.
Найменше значення функції виникає, коли x = 0, де y = 0. Це пояснюється тим, що функція досягає свого мінімального значення при x = 0, а значення y в цій точці дорівнює нулю.
Функція не має максимального значення, оскільки воно необмежено зростає зі збільшенням x. Тому це не має найбільшого значення.
Нарешті, функція є парною, оскільки f(x) = f(-x) для всіх x у R. Щоб зрозуміти чому, давайте замінимо -x замість x у функції:
f(-x) = (-x)² = x² = f(x)
Отже, функція y = x² має такі властивості:
Область визначення: усі дійсні числа
Зростання: необмежено зростає зі збільшенням x, але також необмежено падає зі зменшенням x
Мінімальне значення: виникає при x = 0, зі значенням y = 0
Максимальне значення: не існує, оскільки функція зростає нескінченно
Рівність: Так, функція парна