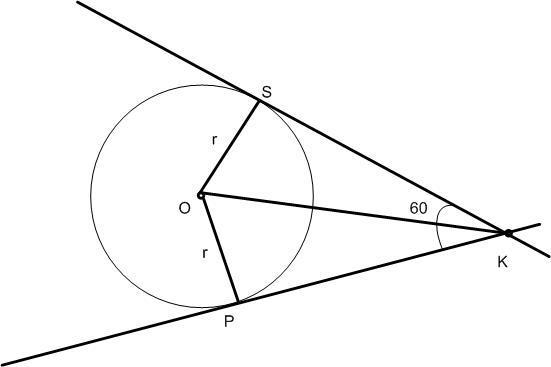
З точки К, що лежить поза колом з центром О проведено дотичні КР і КS. Відомо, що РКS=60°. Знайти радіус цього кола якщо відрізок КО дорівнює 13см
Ответы на вопрос
Ответ:
l r l=6.5 (см)
Объяснение:
Смотрим чертеж:
Это прямоугольные треугольники, т.к. углы ∠КSO=∠KPO=90° (как углы между касательной к окружности и радиусом, проведенным в точку касания - по определению касательной). У этих прямоугольных треугольников равны гипотенузы (они просто совпадают. Это - отрезок ОК), и один из катетов (как радиусы окружности r). Следовательно по условию соответственного равенства гипотенузы и одного из катетов, прямоугольные треугольники равны:
Δ KOS ≡ Δ KOP
У равных треугольников соответствующие углы равны. Следовательно:
∠SKO = ∠PKO следовательно отрезок KO - бисектрисса ∠SKP .
Значит ∠SKO = ∠PKO=60/2=30°.
У прямоугольного треугольника катет, лежащий против угла 30° равен полвине гипотенузы (KO). Против угла ∠SKO (или ∠PKO) лежит катет, равный радиусу окружности r, значит:
l r l=l KO l/2
l r l=13/2=6.5 (см)
Ответ:... Птица,?
Объяснение:
