Якщо периметр квадрата 8√2 см, то радіус кола, описаного навколо квадрата, дорівнює:

Ответ:

Радіус кола, описаного навколо квадрата, дорівнює 2 см

Объяснение:

Якщо периметр квадрата 8√2 см, то чому дорівнює радіус кола, описаного навколо квадрата?

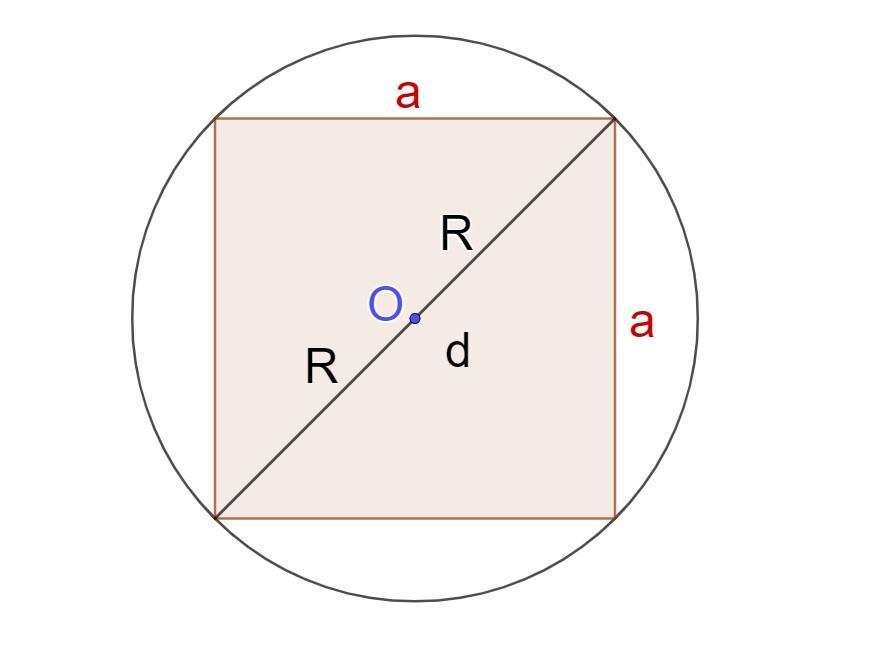
Радіус  кола, описаного навколо квадрата, дорівнює половині його діагоналі.

R=d/2

Оскільки діагональ квадрата можна знайти за формулою:

d=a√2

де а - сторона квадрата, то:

Розв'язання задачі зводиться до знаходження сторони квадрата а.

Відомо, що у квадрата всі сторони рівні, а периметр, за умовою, дорівнює 8√2 см, тоді знайдемо сторону квадрата:

а=Р/4

 (см)

Отже:

 (см)

Відповідь: 2 см

#SPJ1