Алгебра, вопрос задал lizertttt , 6 лет назад

Я не понимаю почему в числителе будет √3(1-√3),откуда появился 1 и √3(тобишь как получилось)

Приложения:

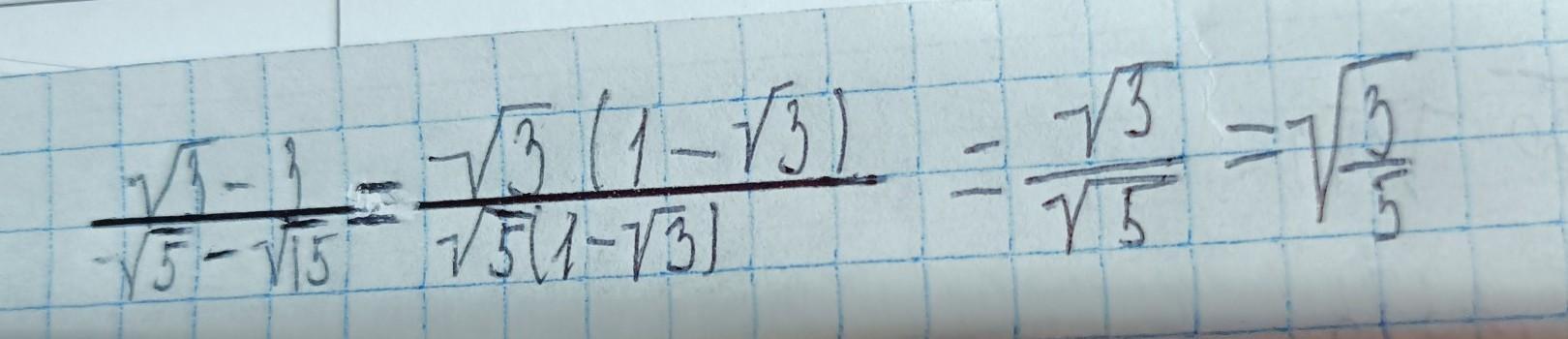
NNNLLL54: вынесли общий мнодитель: корень3-3=корень3- корень3*корень3=корень3*(1-корень3)

Ответы на вопрос

Ответил SoliBes

Ответ:

Рассмотрим числитель: Здесь за скобки для упрощения выражения вынесли корень из трех, соответственно в скобках осталось 1-к3. Откуда взялось? грубо говоря каждое число разделили на корень из трех (корень из трех разделить на корень из трех будет как раз 1, 3 разделить на корень из трех будет корень из трех).

В знаменателе то же самое, там вынесли корень из пяти, то есть каждое число на него разделили, сам корень из пяти вынесли за скобки, а "остаток" оставили в них.

SoliBes: И дополнительно на всякий случай: когда какое-то число делят на квадратный корень этого же числа всегда получается этот самый корень. Так, 7 разделить на корень из семи будет корень из семи и так далее

Ответил natalyabryukhova

Объяснение:

$\displaystyle \frac{\sqrt{3}-3 }{\sqrt{5}-\sqrt{15} }$

Для любых действительных чисел a и b таких, что a ≥0 и b≥0 выполняется равенство $\sqrt{ab}=\sqrt{a}*\sqrt{b}$
Для любого неотрицательного числа a справедливо, что $\sqrt{a}\ge0\ и\ (\sqrt{a})^2=a$
Для любых действительных чисел a и b таких, что a ≥0 и b≥0 выполняется равенство $\displaystyle \frac{\sqrt{a} }{\sqrt{b} } =\sqrt{\frac{a}{b} }$

$\displaystyle \frac{\sqrt{3}-(\sqrt{3})^2 }{\sqrt{5}-\sqrt{3*5} } =\frac{\sqrt{3}-\sqrt{3}*\sqrt{3} }{\sqrt{5}-\sqrt{3} *\sqrt{5} } } =\frac{\sqrt{3}(1-\sqrt{3}) }{\sqrt{{5} }(1-\sqrt{3}) } =\frac{\sqrt{3} }{\sqrt{5} } =\sqrt{\frac{3}{5} }$