y=x^2/(4*x^2-1) нужно полное исследование функции!
Ответы на вопрос
Ответил xxxeol
0
ДАНО
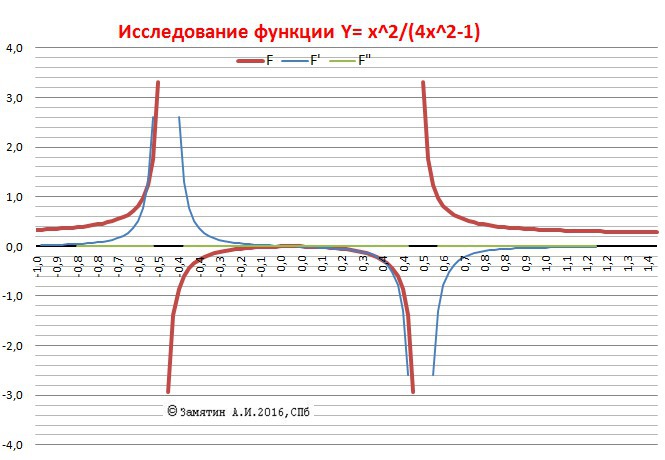
Функция Y = x²/(4x² - 1)
ИССЛЕДОВАНИЕ.
1. Область определения.
4x² - 1 ≠ 0 x ≠ +/- 0.5.
Х∈(-∞,-0,5]∪[-0.5,0.5]∪[0.5,+∞).
2. Пересечение с осью Х - Х=0.
3. Пересечение с осью У - Х=0 и У(0) = 0.
4. Поведение в точках разрыва.
lim(-0.5 -) = +∞ и lim(-0.5 +) = -∞
lim(0.5-) = -∞ и lim(0.5+) = +∞.
5. Поведение на бесконечности.
lim(-∞) = 1/4 lim(+∞) = 1/4.
6. Наклонная асимптота - У= 1/4.
7. Исследование на четность.
У(-х) = У(х) - функция четная.
8. Первая производная - поиск экстремумов.

9. Экстремум - ноль производной - Х=0, Уmax(0) = 0.
10. Возрастает - X∈(-∞,-0.5)∪(-0.5,0].
Убывает - X∈[0,0.5)∪(0.5,+∞).
11. Точек перегиба - нет.
12. График прилагается.
Функция Y = x²/(4x² - 1)
ИССЛЕДОВАНИЕ.
1. Область определения.
4x² - 1 ≠ 0 x ≠ +/- 0.5.
Х∈(-∞,-0,5]∪[-0.5,0.5]∪[0.5,+∞).
2. Пересечение с осью Х - Х=0.
3. Пересечение с осью У - Х=0 и У(0) = 0.
4. Поведение в точках разрыва.
lim(-0.5 -) = +∞ и lim(-0.5 +) = -∞
lim(0.5-) = -∞ и lim(0.5+) = +∞.
5. Поведение на бесконечности.
lim(-∞) = 1/4 lim(+∞) = 1/4.
6. Наклонная асимптота - У= 1/4.
7. Исследование на четность.
У(-х) = У(х) - функция четная.
8. Первая производная - поиск экстремумов.
9. Экстремум - ноль производной - Х=0, Уmax(0) = 0.
10. Возрастает - X∈(-∞,-0.5)∪(-0.5,0].
Убывает - X∈[0,0.5)∪(0.5,+∞).
11. Точек перегиба - нет.
12. График прилагается.
Приложения:
Ответил tva1998
0
большое спасибо!
Новые вопросы