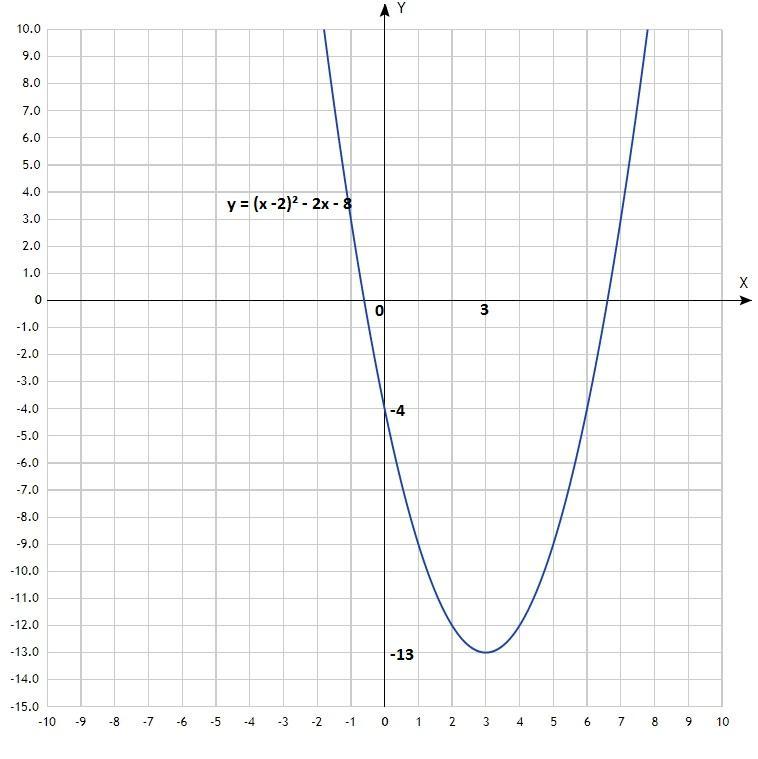
y= x-2^2 -2x-8 (исследовать) 1.направление ветвей
2.координаты вершины
3. нули функции
4. точка пересечения с Оy
5. Д(у)
6. Е(у)
Ответы на вопрос
Ответ:
В решении.
Объяснение:
y = (x -2)² - 2x - 8; (исследовать):
1. Направление ветвей:
ветви параболы направлены вверх, коэффициент перед х² > 0;
2. Координаты вершины:
а) Преобразовать уравнение функции:
y = (x -2)² - 2x - 8;
у = х² - 4х + 4 - 2х - 8
у = х² - 6х - 4
б) Найти х₀ по формуле:
х₀ = -b/2а;
х₀ = 6/2
х₀ = 3;
в) Найти у₀:
подставить значение х₀ в уравнение функции и вычислить у₀:
у = х² - 6х - 4
у₀ = 3² - 6 * 3 - 4 = 9 - 18 - 4 = -13
у₀ = -13;
Координаты вершины параболы: (3; -13).
3. Нули функции - значения х, при которых парабола пересекает ось Ох.
Приравнять уравнение к нулю и решить квадратное уравнение:
х² - 6х - 4 = 0
D=b²-4ac = 36 + 16 = 52 √D=√52 =√(4*13) = 2√13;
х₁=(-b-√D)/2a
х₁=(6-2√13)/2
х₁=3-√13; (≈ -0,6);
х₂=(-b+√D)/2a
х₂=(6+2√13)/2
х₂=3+√13; (≈ 6,6);
Нули функции: х₁=3-√13; х₂=3+√13;
4. Точка пересечения с Оy:
Любой график пересекает ось Оу при х = 0:
у = х² - 6х - 4; х = 0;
у = 0² - 6*0 - 4
у = -4;
Координаты точки пересечения параболой оси Оу: (0; -4).
5. Д(у) - область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.
Запись: D(у) = R, или D(у) = х∈(-∞; +∞).
6. Е(у) - область значений параболы определяется значением ординаты вершины (у₀).
у₀ = -13, ветви параболы направлены вверх, значит, у = -13 наименьшее значение функции.
Тогда область значений функции Е(у) = у∈[-13; +∞).