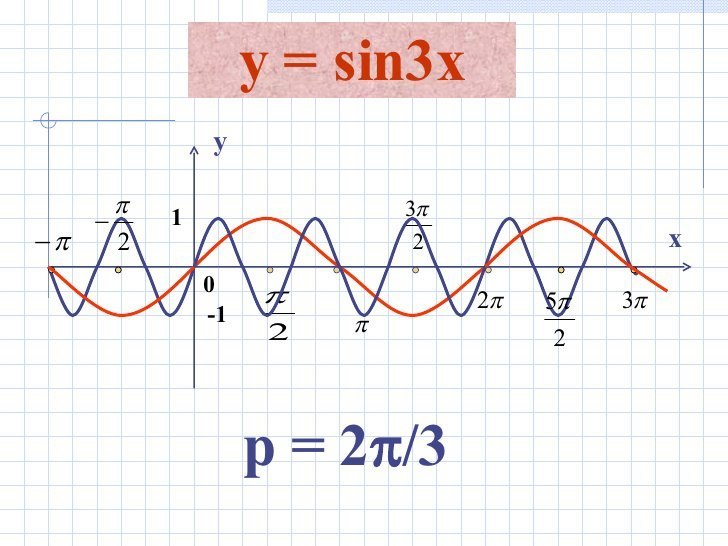
Y=sin3x
Распишите решение пожалуйста,с пояснением и все дела
Приложения:
Ответы на вопрос
Ответил WhatYouNeed
0
Решение:
У функции f(x)=sin x период 2π, поэтому у функции y=sin3x период 2π÷3 = т.к. коэффициент перед х больше 1 и равен 3.
Ответ:
Объяснение:
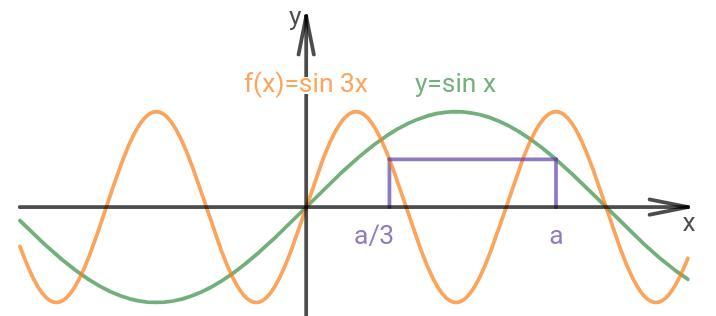
Объясню через простейшие преобразования графиков.
Найдём ординату (O₁) функции у для a/3:
Найдём ординату (O₂) функции f для a:
Как видно O₁ = O₂ . График функции y отличается от графика функции f тем, что он сжат в 3 раза по оси Ox, то есть для каждой точки графика фун. f ордината осталось той же, а абсцисса уменьшилась в 3 раза.
Период у функции это константа, на графике у функции с периодом верно следующее: если абсциссы точек отличаются на t·k, где t - период; k - целое, то ординаты этих точек равны.
А раз абсциссы точек уменьшились в 3 раза, то период тоже в 3 раза.
Приложения:
Новые вопросы
Математика,
2 года назад
Химия,
8 лет назад
Математика,
8 лет назад
Биология,
9 лет назад
Математика,
9 лет назад