Y=sin3x
Распишите решение пожалуйста,с пояснением и все дела
Приложения:
Ответы на вопрос
Ответил NNNLLL54
0
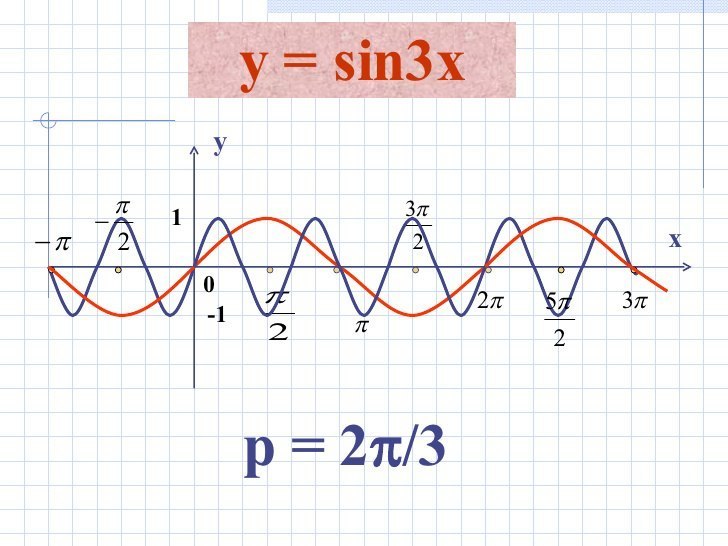
Чтобы построить график функции y=sin3x , надо сжать график у=sinx вдоль оси ОХ в 3 раза.
Сначала на графике построен график функции y=sinx . Он начерчен коричневым цветом. Нули функция имеет в точках -П , 0, П , 2П, 3П ,...
Функция y=sin3x будет иметь нули в 3 раза чаще, то есть в точках
-П , -2П/3 , -П/3 , 0 , П/3 , 2П/3, П , 4П/3 , ...
Значения самой же функции будут изменяться так же: -1<sin3x<1 .
Наименьший положительный период функции , как видно по чертежу, равен р=2П/3 .
Максимальные значения функция у=sin3x принимает в точках ,
где выполняется равенство sin3x=1 ,
то есть при 3х=П/2+2Пn ⇒ х= П/6+2Пn/3 , n∈Z .
Минимальные значения функция принимает ,если sun3x= -1,
то есть при 3х= -П/2+2Пn ⇒ х= -П/6+2Пn/3 , n∈Z .
Всё это можно проверить, если придавать переменной х числовые значения.
Например, х=П/3 ⇒ sin(3·П/3)=sinП=0
х=2П/3 ⇒ sin(3·2П/3)=sin(2П)=0
х=П ⇒ sin(3П)=0
х=П/6 ⇒ sin(3·П/6)=sinП/2=1
х=П/2 ⇒ sin(3·П/2)= -1
Сначала на графике построен график функции y=sinx . Он начерчен коричневым цветом. Нули функция имеет в точках -П , 0, П , 2П, 3П ,...
Функция y=sin3x будет иметь нули в 3 раза чаще, то есть в точках
-П , -2П/3 , -П/3 , 0 , П/3 , 2П/3, П , 4П/3 , ...
Значения самой же функции будут изменяться так же: -1<sin3x<1 .
Наименьший положительный период функции , как видно по чертежу, равен р=2П/3 .
Максимальные значения функция у=sin3x принимает в точках ,
где выполняется равенство sin3x=1 ,
то есть при 3х=П/2+2Пn ⇒ х= П/6+2Пn/3 , n∈Z .
Минимальные значения функция принимает ,если sun3x= -1,
то есть при 3х= -П/2+2Пn ⇒ х= -П/6+2Пn/3 , n∈Z .
Всё это можно проверить, если придавать переменной х числовые значения.
Например, х=П/3 ⇒ sin(3·П/3)=sinП=0
х=2П/3 ⇒ sin(3·2П/3)=sin(2П)=0
х=П ⇒ sin(3П)=0
х=П/6 ⇒ sin(3·П/6)=sinП/2=1
х=П/2 ⇒ sin(3·П/2)= -1
Новые вопросы
Алгебра,
2 года назад
Математика,
2 года назад
Химия,
8 лет назад
История,
8 лет назад
Химия,
9 лет назад