Y=sin3x
Распишите решение пожалуйста,с пояснением и все дела

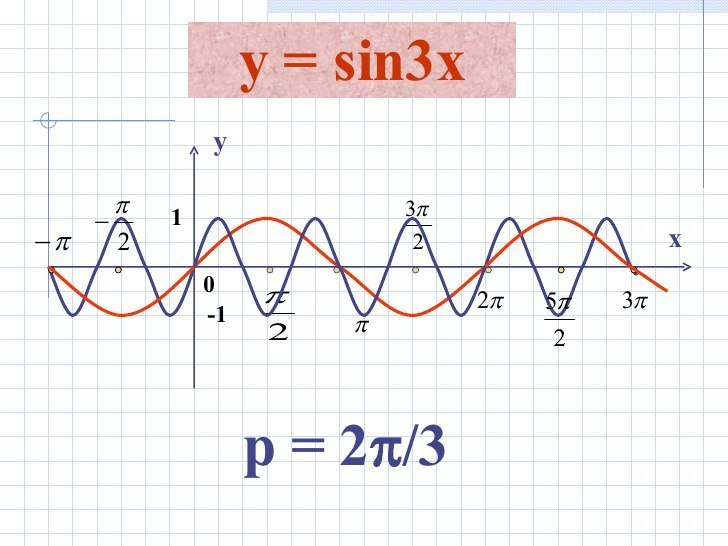
Есть классическая функция у=sinx её период равен 2П, то есть каждые 2П или 360 градусов её значения повторяются. Если перед х стоит коэффициент, то он меняет период функции, то есть она все свои значения показывает на участке 2П/к.
Если 0<к<1, то она растягивается, если к>1, то она сжимается.
В данном случае к=3, то есть за период 2п она в 3 раза сожмётся. Её период становится р=360/3=120 градусов или р=2*П/3. И на участке в 2П она 3 раза повторится.

Решение:

Пусть Р – основной период функции Y=sin3x .

Положим f(x) = sin3x

f(x) + Р = sin3(x + Р) = sin(3x + 3Р)

3Р = 2π 

Основной период функции равен:

Р = 2π/3