Математика, вопрос задал Dark1 , 9 лет назад

Высшая математика! Найти производную второго порядка. С полным ходом решения пожалуйста.

Приложения:

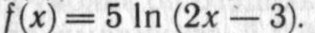
Ответы на вопрос

Ответил CVita

вспоминаем таблицу основных производных
$(lnx)'= frac{1}{x} \ ( frac{1}{x})'=(x^-^1)'=-x^-^2=- frac{1}{x^2}$
а теперь применяя правила нахождения производных сложных функций найдем то, что нам надо
$(5ln(2x-3)'=5(ln(2x-3))'*(2x-3)'=5* frac{1}{2x-3}*2= frac{10}{(2x-3)} \ (5ln(2x-3))''=( frac{10}{(2x-3)})'=(10*(2x-3)^-^1)'*(2x-3)'= \ 10*(-(2x-3)^-^2)*2=- frac{20}{(2x-3)^2}$
вот и все

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 2 года назад

Помогите пж,номер 4 и 5 с объяснениями...

Английский язык, 2 года назад

Задайте в каждому предложению общий вопрос (с did) 1)Anne Hathaway and the couple had three children. 2)A few years after his marriage, Shakespeare moved to London where he worked as both a...

Литература, 9 лет назад

разве тот счастлив ,кто счастлив один?

Математика, 9 лет назад

Мотоциклист расстояние между двумя населёнными пунктами проехал за 1 час 24 минуты со скоростью 40км/ч .Расстояние между этими населёнными пунктами изображено на карте отрезком длиной 4см.Найдите...

Литература, 9 лет назад

Цитаты характеризующие состояние Троекурова после суда??

Обществознание, 9 лет назад

Выдающиеся личности присущи такие качества как... (Помогите плиз, срочно)...