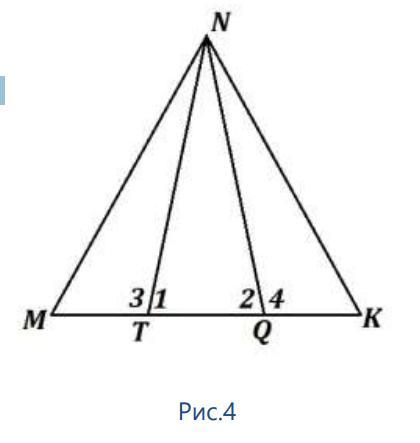
Высота треугольника MNK
является медианой треугольника TNQ,
MT=QK (рис.4). Докажите, что треугольник
MNK равнобедренный. Найдите ∠3, если
∠2 + ∠1 − ∠4 = 30°

Ответ:

110°

Объяснение:

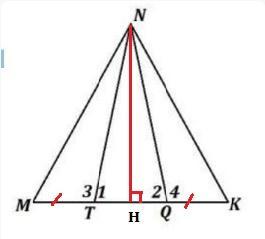
1) NH - медиана ΔTNQ ⇒ по свойству медианы TH=HQ.

По условию MT=QK ⇒ МH=HK, т.к. сумма равных отрезков даёт в итоге равные отрезки: MT+TH = QK+HQ. ⇒ NH - медиана ΔMNK.

По условию задачи NH - высота ΔMNK.

• Если в треугольнике медиана и высота, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный.

⇒ ΔMNK - равнобедренный, что и  требовалось доказать.

ΔTNQ также равнобедренный, т.к. NH - медиана и высота.

2) ∠2 + ∠1 − ∠4 = 30°

∠2=∠1, т.к. у равнобедренного ΔTNQ углы при основании равны.

По свойству смежных углов: ∠4 = 180°-∠2 , но ∠2=∠1, поэтому ∠4=180°-∠1

⇒ ∠1+∠1-(180°-∠1)=30°

3*∠1=30°+180°

3*∠1=210°

∠1=70°

По свойству смежных углов: ∠3=180°-∠1=180°-70°=110°