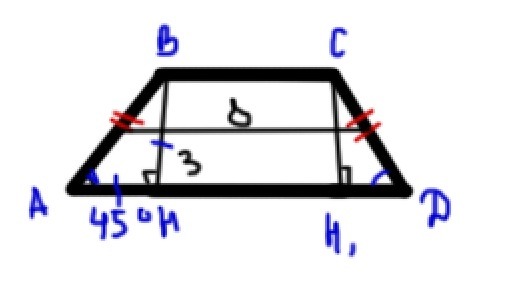
Высота равнобедренной трапеции равна 3 см, средеюняя линия трапеции равна 8 см. Острый угол трапеции равен 45°. Вычислить все стороны трапеции и ее площадь.
СРОЧНО НАРОД, ХЕЛП!!!
Ответы на вопрос
Ответил Аноним
0
Имеем два равных прямоугольных треугольника.
Они равны по второму признаку. Гипотенузы ,катет (высота трапеции) и угол между ними - равны
В прямоугольном треугольнике, у которого углы равны по 45 градусов- катеты равны.
(острый угол трапеции является острым угол прямоугольного треугольника).
Это означает, что отрезки HA=H1D равны катету СН1=ВН=3
Теперь мы можем найти боковые стороны, и основания.
По теореме Пифагора квадрат длинны гипотенузы равен сумме квадратов двух его катетов CD^2=AB^2=3^2+3^2 =18
CD=AB= =
=
Теперь найдем основания.
Пусть отрезок ВС=х тогда АD=x+3+3=x+6
Тк из точек B и C опущены перпендикуляры
Теперь нужно решить несложное уравнение.
Длинна средней линии трапеции равна полусумме двух её оснований:
8=((x+x+6):2)
16=2х+6
10=2х
х=5
Площадь.
По одной из формул площадь трапеции равна высоте этой трапеции умноженной на среднюю линию
те Sabcd=3*8=24
Они равны по второму признаку. Гипотенузы ,катет (высота трапеции) и угол между ними - равны
В прямоугольном треугольнике, у которого углы равны по 45 градусов- катеты равны.
(острый угол трапеции является острым угол прямоугольного треугольника).
Это означает, что отрезки HA=H1D равны катету СН1=ВН=3
Теперь мы можем найти боковые стороны, и основания.
По теореме Пифагора квадрат длинны гипотенузы равен сумме квадратов двух его катетов CD^2=AB^2=3^2+3^2 =18
CD=AB=
Теперь найдем основания.
Пусть отрезок ВС=х тогда АD=x+3+3=x+6
Тк из точек B и C опущены перпендикуляры
Теперь нужно решить несложное уравнение.
Длинна средней линии трапеции равна полусумме двух её оснований:
8=((x+x+6):2)
16=2х+6
10=2х
х=5
Площадь.
По одной из формул площадь трапеции равна высоте этой трапеции умноженной на среднюю линию
те Sabcd=3*8=24
Приложения:
Ответил beleve
0
Спасибо Вам
Новые вопросы
Английский язык,
2 года назад
Қазақ тiлi,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад