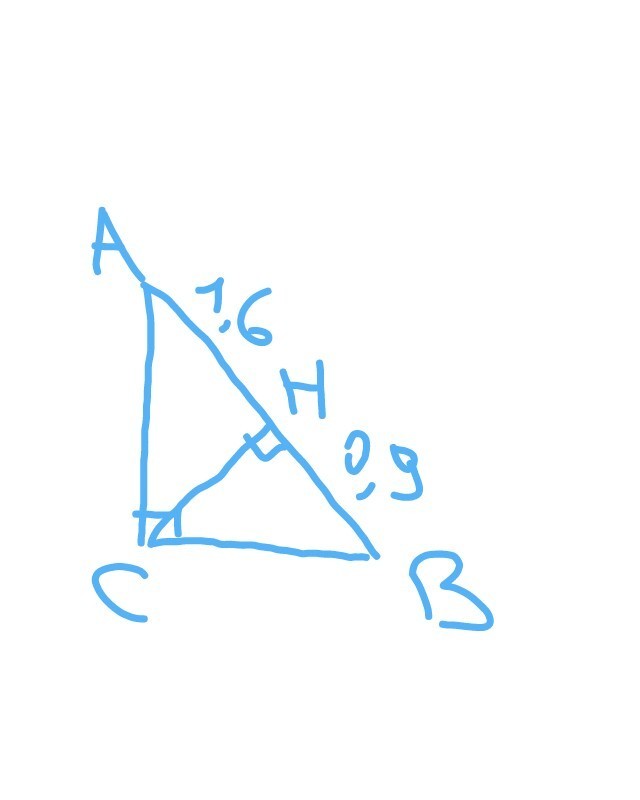
Высота, проведённая к гипотенузе прямоугольного треугольника, делит её на части длиной 1,6 и 0,9. Найдите площадь прямоугольного треугольника.
Ответы на вопрос
Ответил snow99
0
Треугольник ACH подобен треугольнику ABC по двум углам (угол A - общий и угол ACB = угол AHC = 90°).
Треугольник BCH подобен треуг. ABC по двум углам (угол С - общий, угол BHC = угол ACB = 90°).
Значит, и треугольники ACH и BCH подобные.
Тогда:
BH/CH = CH/AH
CH^2 = AH * HC = 1,6 * 0,9 = 1,44
CH = 1,2 (см)
AB = 1,6 + 0,9 = 2,5 (см)
S = 1/2 * AB * CH = 1/2 * 2,5 * 1,2 = 1,5 (см^2)
Ответ: 1,5 см^2.
Треугольник BCH подобен треуг. ABC по двум углам (угол С - общий, угол BHC = угол ACB = 90°).
Значит, и треугольники ACH и BCH подобные.
Тогда:
BH/CH = CH/AH
CH^2 = AH * HC = 1,6 * 0,9 = 1,44
CH = 1,2 (см)
AB = 1,6 + 0,9 = 2,5 (см)
S = 1/2 * AB * CH = 1/2 * 2,5 * 1,2 = 1,5 (см^2)
Ответ: 1,5 см^2.
Приложения:
Новые вопросы