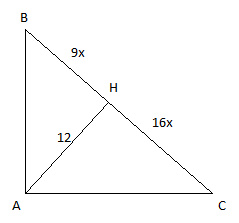
Геометрия, вопрос задал Аноним , 1 год назад

Высота AH прямоугольного треугольника ABC делит гипотенузу BC в отношении 9/16. Найдите длину катетов, если длина высоты равна 12.
с рисунком

Ответы на вопрос

Ответил tanya2512

Рисунок простой: прямоугольный треугольник АВС,угол А=90°, высота АН=12 из прямого угла к гипотенузе.
Решение:
ВН/НС=9/16, ВН=9НС/16
АН=√ВН*НС=√9НС²/16=3НС/4
НС=4АН/3=4*12/3=16
тогда ВН=9*16/16=9
По т.Пифагора катет АС=√АН²+НС²=√12²+16²=√400=20
Катет АВ=√АН²+ВН²=√12²+9²=√225=15
Ответ: 20 и 15

Ответил Аноним

Пусть коэффициент пропорциональности будет х, тогда BH = 9x и CH = 16x
гипотенуза ВС = 9x+16x=25x

Ищем катеты)

$AB^2=BH\cdot BC\\AB= \sqrt{BH\cdot BC} = \sqrt{9x\cdot 25x}= 15x \\ \\ AC^2=CH\cdot BC \\ AC= \sqrt{CH \cdot BC} = \sqrt{16 x\cdot 25 x} =20 x$

Найдем коэффициент пропорциональности через х
$AH^2= BH\cdot CH \\ AH^2=9x\cdot 16x \\ 12^2=144x \\ x=1$

Итак, катеты будут АВ = 15х=15, AC=20

Ответ: 15 и 20.

Приложения: