Вычислите значения остальных тригонометрических функций угла Альфа
Приложения:

Ответы на вопрос
Ответил mathkot
2
Ответ:
Тангенс альфа равен
Косинус альфа равен -0,6
Синус альфа равен 0,8
Объяснение:
(угол α задан в радианах)
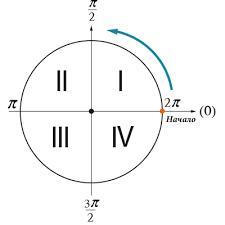
Так как можно считать, что , то угол α находится или во второй или в первой четверти, а так как по условию котангенс меньше нуля, то угол α находится во второй четверти.
Знаки тригонометрических функция во второй четверти:
- sin α > 0
- cos α < 0
- tg α < 0
По тождеству , то есть
По следствию из основного тригонометрического тождества:
По основному тригонометрическому тождеству:
.
Приложения:
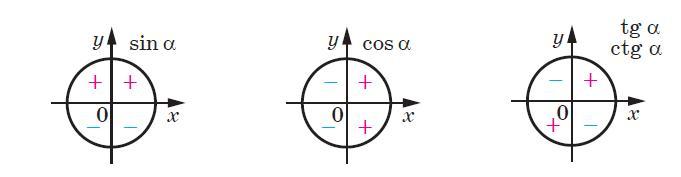
Новые вопросы