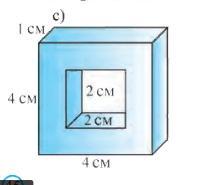
вычислите полную поверхность многогранника, изображенном на рисунке
Ответы на вопрос
Ответ:
Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов:
S=
=2(5 умножить на 1 плюс 7 умножить на 1 плюс 7 умножить на 5) плюс 2(1 умножить на 1 плюс 2 умножить на 1 плюс 2 умножить на 1) минус 4(2 умножить на 1)=
=96.
Ответ: 96.
Объяснение:
9/12 ₽/'1₽!'08#!'0=#!#standoff2' #09'! ##'
Ответ:
Объяснение:
Он имеет две грани с площадью 4⋅4, две грани с площадью 4⋅1 и две грани с площадью 1•4. Следовательно, площадь его поверхности равна 2(4⋅4+4⋅1+1•4)=48. Из этого параллелепипеда вырезали прямоугольный параллелепипед с ребрами 2, 2 и 1. В результате этого площадь боковой поверхности уменьшилась на 1⋅(2⋅2) и увеличилась на 4⋅(1⋅2). Следовательно, площадь поверхности многогранника, изображенного на рисунке, равна