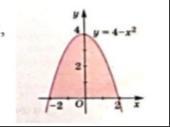
Вычислите площадь заштрихованной фигуры,
изображённой на рисунке

madiarm474: Заметим, что фигура симметрична относительно оси OY.

Тогда площадь можно найти, удвоив площадь:

S_1 = \int\limits^2_0 {(4-x^2)} \, dx = (4x - \frac{x^3}{3})~|_0^2= 4\cdot2 - \frac{2^3}{3}= 8-\frac{8}{3} = \frac{16}{3}S
1
​
=
0
∫
2
​
(4−x
2
)dx=(4x−
3
x
3

​
) ∣
0
2
​
=4⋅2−
3
2
3

​
=8−
3
8
​
=
3
16
​


S = 2·S₁

\begin{gathered}S = 2\cdot \frac{16}{3}= \frac{32}{3}\\\end{gathered}
S=2⋅
3
16
​
=
3
32
​

​

dedulja66let: :((( А это как написать??? :)))

dedulja66let: \begin{gathered}S = 2\cdot \frac{16}{3}= \frac{32}{3}\\\end{gathered} ????