Вычислите площадь поверхности куба по площади его диагонального сечения 13см^2
Помогитееее срочнооо
orjabinina:
78/√2=38√2( см²)
Ответы на вопрос
Ответил ldglkva
1
Ответ:
Площадь поверхности куба равна 39√2 см².
Объяснение:
Вычислить площадь поверхности куба по площади его диагонального сечения 13 см².
- Куб - это прямоугольный параллелепипед, у которого все грани квадраты.
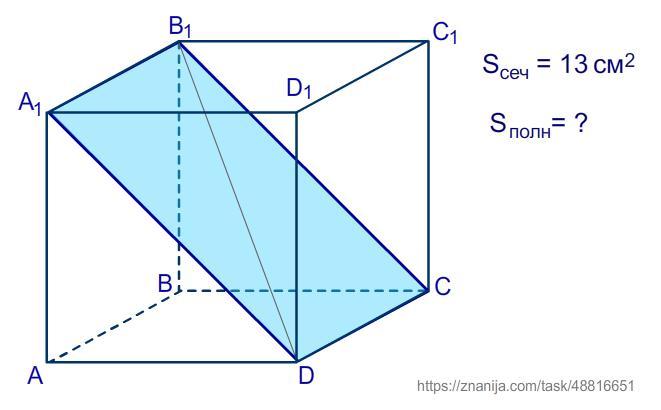
- Диагональное сечение куба - это сечение куба плоскостью, проходящей через диагональ куба и два противолежащих его ребра.
- Диагональное сечение куба представляет собой прямоугольник, меньшие стороны которого совпадают с ребром куба, а большие стороны - с диагональю грани куба.
- Площадь прямоугольника равна произведению двух его смежных сторон.
1) Пусть ребро куба равно см.
Диагональ квадрата со стороной см равна
см (из т.Пифагора).
Тогда диагональное сечение куба - это прямоугольник A₁B₁CD со сторонами см и
см.
2) S(A₁B₁CD) = 13 см² по условию.
(см²)
Квадрат ребра куба:
3) Площадь поверхности куба равна сумме площадей всех его граней.
(см²).
Площадь поверхности куба равна 39√2 см².
Приложения:
Новые вопросы