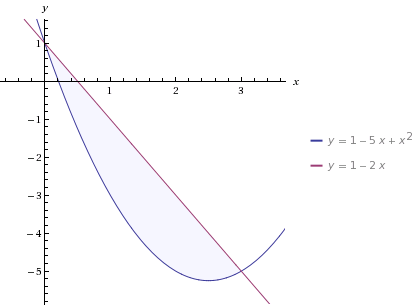
Математика, вопрос задал Adgjmpt9 , 9 лет назад

вычислите площадь фигуры ограниченной линиями y=х^2 -5х +1, y =1 - 2х

Ответы на вопрос

Ответил АннаАрт
0
left { {{y=x^2 -5x +1} atop {y =1 - 2x}} right. \ \ x^2 -5x +1=1 - 2x \ x^2 -3x=0 \ x_{1}=0, x_{2}=3 \ \ A(0;1),B(3;-5) \ \ S=intlimits^b_a {f(x)} , dx =intlimits^b_a {f_{2}(x)-f_{1}(x)} , dx \ \ 1 - 2x-(x^2 -5x +1)=1 - 2x-x^2 +5x -1=3x-x^2 \ \ S=intlimits {(3x-x^2)} , dx= frac{3x^2}{2} - frac{x^3}{3}+const \ \ S=intlimits^3_0 {(3x-x^2)} , dx=frac{9}{2}=4,5
Приложения:
Предыдущий вопрос
Следующий вопрос
Новые вопросы