Вычислите площадь фигуры, ограниченной линиями y=4x-x^2 и y=3.
Ответы на вопрос
Ответил NNNLLL54
1
Ответ: .
Объяснение:
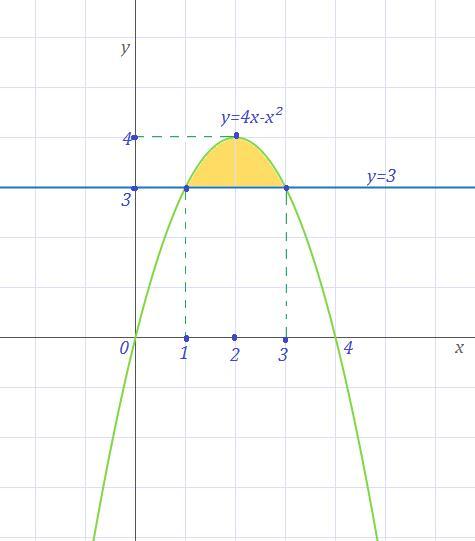
y=4x-x² - парабола, ветви вниз, точки пересечения с ОХ: (0,0) и (4,0) , вершина в точке (2,4) .
у=3 - прямая, параллельная оси ОХ, проходящая через точку (0,3). Точки пересечения параболы и прямой:
Приложения:
Ответил Аноним
1
Графиком первой функции будет парабола, ветвями вниз, второй - прямая, параллельная оси ох, проходящая через точку (0;3)
Площадь фигуры, огранич. этими линиями считаем как определенный интеграл от разности(4х-х²-3). Найдем пределы интегрирования и подставим их в функцию 2х²-х³/3-3х.
4x-x² =3. 4x-x² -3=0 х²-4х+3=0. по теореме, обратной теореме Виета корнями будут 1 и 3. По формуле Ньютона - Лейбница найдем определенный интеграл 2*9-27/3-3*3-(2*1-1/3-3)=3+1/3-2=1 целая 1/3
Аноним:
пожалуйста
Новые вопросы