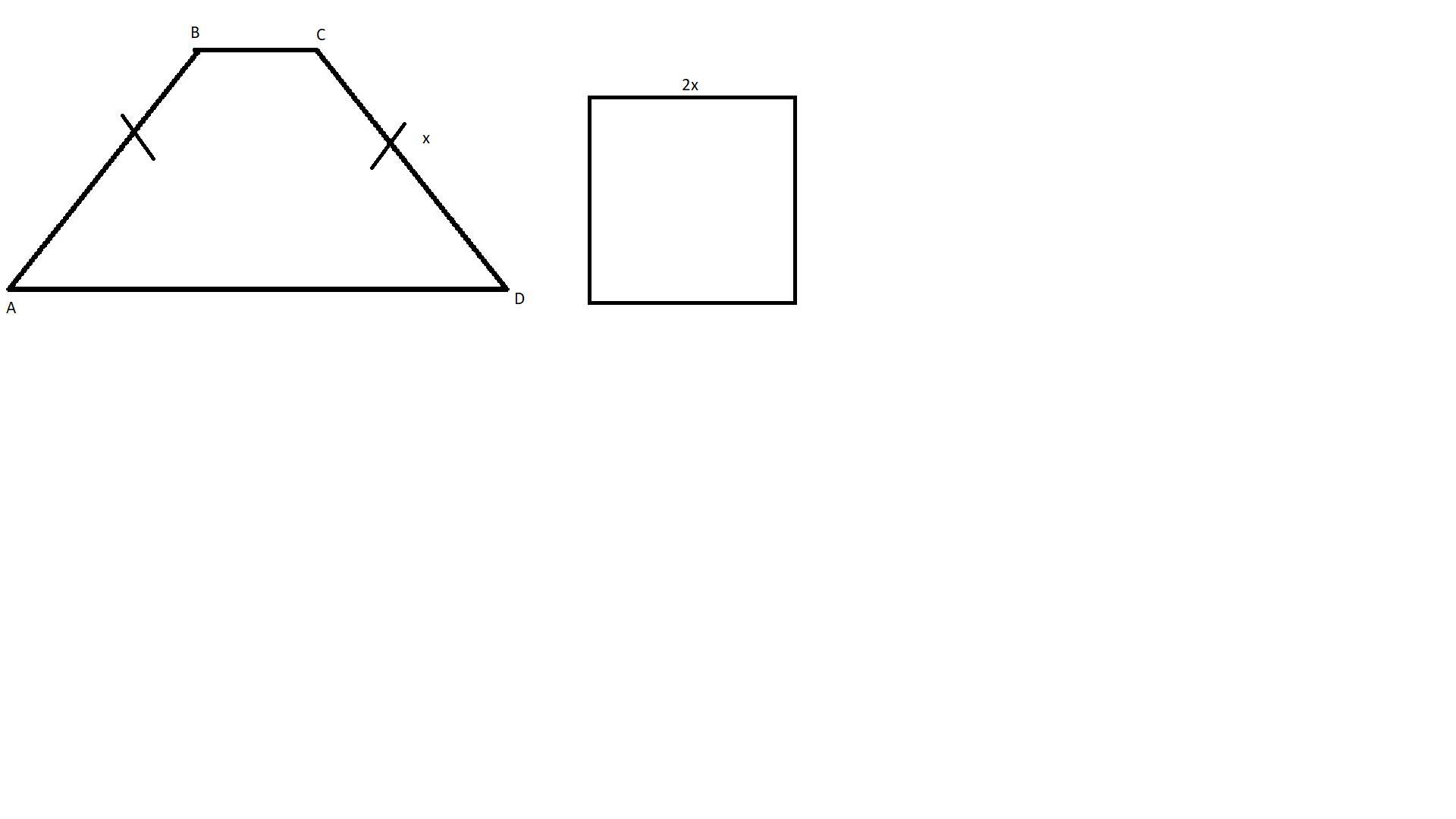
Вычислите периметр квадрата, сторона которого вдвое больше наклонной стороны равнобедренной трапеции с периметром 72 см и суммой измерений оснований, равной сумме измерений наклонных сторон.​

Ответ:

Периметр квадрата равен 144 см.

Пошаговое объяснение:

Рассмотрим равнобедренную трапецию ABCD.

Так как сумма измерений оснований равна сумме измерений наклонных сторон, а периметр равен 72 см, то:

AB+CD=AD+BC=72:2=36 (см)

AB=CD=36:2=18 (см) - так как в равнобедренной трапеции боковые стороны равны.

Рассмотрим квадрат.

Так как его сторона вдвое больше наклонной стороны трапеции, что равно 18 см, то:

18*2=36 (см) - длина стороны квадрата.

Периметр квадрата: 36*4=144 (см).