Алгебра, вопрос задал xgamerxpowerp9qy5j , 1 год назад

Вычислите! "Корни n-ой степени из числа"

Приложения:

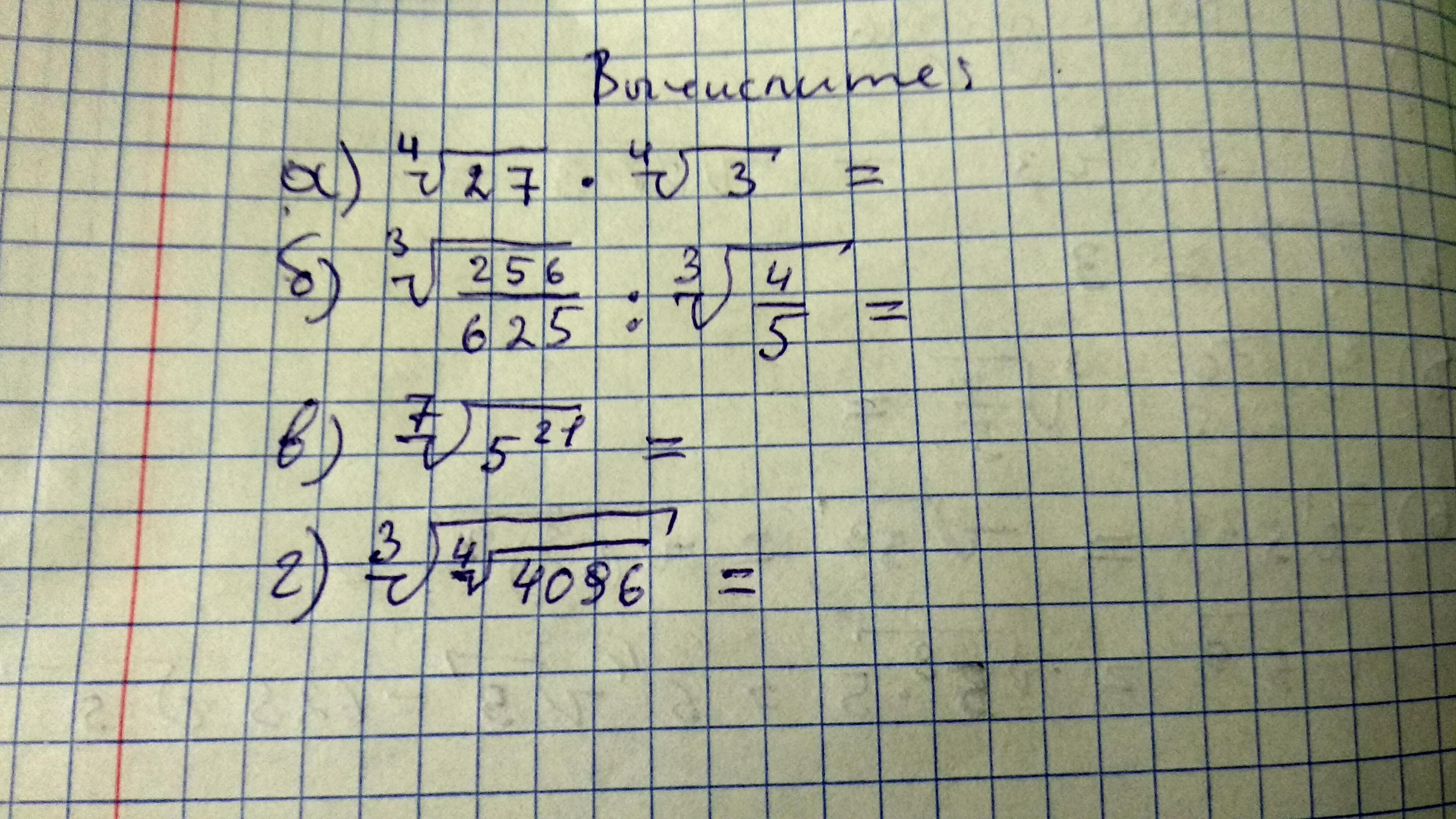
Ответы на вопрос

Ответил Universalka

0

$1)\sqrt[4]{27}*\sqrt[4]{3}=\sqrt[4]{27*3}=\sqrt[4]{3^{3}*3 }=\sqrt[4]{3^{4}}=3\\\\Otvet:\boxed{3}\\\\2)\sqrt[3]{\frac{256}{625}}:\sqrt[3]{\frac{4}{5}}=\sqrt[3]{\frac{256}{625}*\frac{5}{4}}=\sqrt[3]{\frac{64}{125}}=\sqrt[3]{\frac{4^{3}}{5^{3}}}=\frac{4}{5}=0,8\\\\Otvet:\boxed{0,8}\\\\3)\sqrt[7]{5^{21}}=\sqrt[7]{(5^{3})^{7}}=5^{3}=125\\\\Otvet:\boxed{125}$

$4)\sqrt[3]{\sqrt[4]{4096}}=\sqrt[12]{4096}=\sqrt[12]{2^{12}}=2\\\\Otvet:\boxed{2}$

xgamerxpowerp9qy5j: Благодарю за подробное решение!

Ответил 25hjoerf10

0

а)

$\sqrt[4]{27} *\sqrt[4]{3} =\sqrt[4]{27*3} =\sqrt[4]{3^{3}*3}=\sqrt[4]{3^{4}} =3$

б)

$\sqrt[3]{\frac{256}{652}}:\sqrt[3]{\frac{4}{5}}=\sqrt[3]{\frac{4^{4} }{5^{4} } } </strong><strong>:</strong><strong>\sqrt[3]{\frac{</strong><strong>4</strong><strong>}{</strong><strong>5</strong><strong>} } =\sqrt[3]{\frac{4^{3}*4}{5^{3}*5}} </strong><strong>:</strong><strong>\sqrt[3]{\frac{</strong><strong>4</strong><strong>}{</strong><strong>5</strong><strong>} } =\frac{4}{5}\sqrt[3]{\frac{</strong><strong>4</strong><strong>}{</strong><strong>5</strong><strong>} }:\sqrt[3]{\frac{</strong><strong>4</strong><strong>}{</strong><strong>5</strong><strong>} } =\frac{4}{5}=0,8$

в)

$\sqrt[7]{5^{21} } =\sqrt[7]{(5^{3})^{7}}=5^{3} =125$

г)

$\sqrt[3]{\sqrt[4]{4096} } =\sqrt[3*4]{4096} =\sqrt[12]{4096} =\sqrt[12]{2^{12} }=2$

xgamerxpowerp9qy5j: Благодарю за подробное решение!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 1 год назад

поставте іменники в орудному відмінку однини, обґрунтуйте написання.

Математика, 1 год назад

обчисліть |-3,24+1-1,91-11,25= помогите ...

География, 1 год назад

Перші і достовірні відомості про Китай європейці отримали після подорожі А) вікінгів Б) Васко Да Гами В) Марко Поло Г) Христофор Колумб...

Українська мова, 1 год назад

В усіх реченнях одиничний дієприслівник відокремлюється комами, окрім (розділові знаки пропущені). А) Розбудовуючись Київ зумів лишити живу природу найбільшою своєю окрасою. Б) Опритомнівши...

Алгебра, 6 лет назад

0,004p²- 1,69q².....

Математика, 6 лет назад

пожалуйста помогите,5 класс на фото задание...