Математика, вопрос задал Kairat013 , 1 год назад

Вычислите интеграл 4 задание

Приложения:

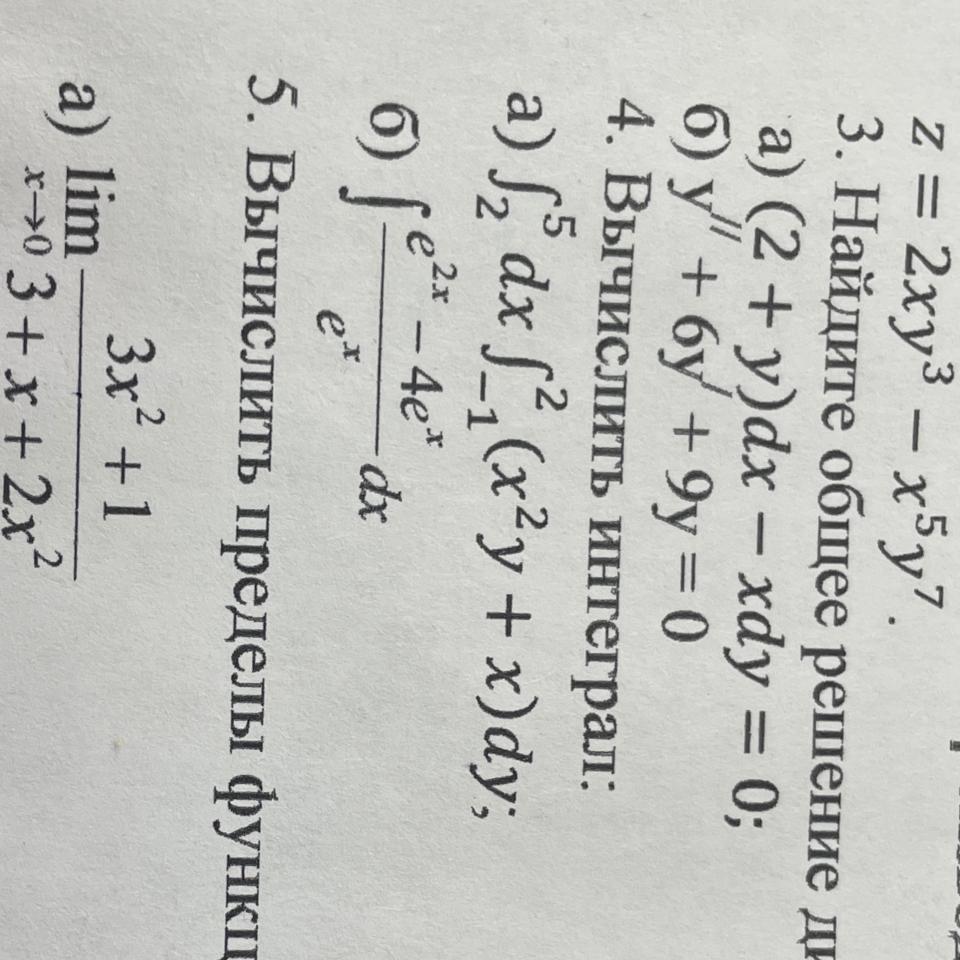
Ответы на вопрос

Ответил NNNLLL54

1

Ответ:

Вычислить повторный интеграл :

$\bf 1)\displaystyle \ \ \int\limits_2^5\, dx\int\limits_{-1}^2(x^2y+x)\, dy=\int\limits_2^5\, dx\Big(x^2\cdot \frac{y^2}{2}+x\, y\Big)\Big|_{-1}^2=\\\\\\=\int\limits_2^5\Big(2x^2+2x-\dfrac{1}{2}\, x^2+x\Big)\, dx=\Big(\frac{3}{2}\cdot\frac{x^3}{3}+3\cdot \frac{x^2}{2}\Big)\Big|_2^5=\\\\\\=\frac{5^3}{2}+\frac{3}{2}\cdot 5^2-\frac{2^3}{2}-\frac{3}{2}\cdot 2^2=\frac{125}{2}+\frac{75}{2}-\frac{8}{2}-\frac{12}{2}=\frac{180}{2}=90$

$\bf 2)\ \ \displaystyle \int \frac{e^{2x}-4e^{x}}{e^{x}}\, dx=\int \Big(\, e^{x}-4\Big)\, dx=e^{x}-4x+C$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 11 месяцев назад

4.До l дієвідміни належать дієслова,які в 3-й особі множини мають закінчення: а)-ать, -ять б)-уть, -ють...

Английский язык, 11 месяцев назад

1/Open the brackets. If you (hurry), you (catch) the bus. If you don’t hurry, you will catch the bus. If you hurry, you will not catch the bus. If you hurry, you catches the bus. If...

Физика, 1 год назад

Через участок цепи идёт постоянный ток. Сила тока I = 15А. Какую силу тока показывает амперметр? Сопротивление амперметра не учитывайте...

Английский язык, 1 год назад

Look at the words in bold in the sentences (1-8) that the speakers used in exercise 3. Match them with their definitions (a-h)...

Алгебра, 6 лет назад

помогите срочно умоляю...

Математика, 6 лет назад

ПОМОГИТЕ ПОЖАЛУЙСТА; найдите корень уравнения: 5/6у-3/4у+1=-1/6...