Математика, вопрос задал Infalible , 7 лет назад

Вычислите двойной интеграл по области D.

Приложения:

Ответы на вопрос

Ответил triggerbott

Область интегрирования смотрите на фото. Разобъем данную область прямой y = 0 и будем считать как сумму двух интегралов

$displaystyle iintlimits_D (3x+y+2)dxdy=intlimits^0_{-1}dyintlimits^{1}_{y^2}(3x+y+2)dx+intlimits^{2}_{0}dyintlimits^1_{frac{y}{2}}(3x+y+2)dx=\ \ \ =intlimits^0_{-1}left(xy+dfrac{3x^2}{2}+2xright)bigg|^1_{y^2}dy+intlimits^2_0left(xy+dfrac{3x^2}{2}+2xright)bigg|^1_{frac{y}{2}}dy=\ \ \ =intlimits^0_{-1}left(-dfrac{3y^4}{2}-y^3-2y^2+y+dfrac{7}{y}right)dy+intlimits^2_0left(dfrac{7}{2}-dfrac{7y^2}{8}right)dy=$

$=displaystyle left(-dfrac{7y^5}{10}-dfrac{y^4}{4}-dfrac{2y^3}{3}+dfrac{y^2}{2}+dfrac{7y}{2}right)bigg|^0_{-1}+left(dfrac{7y}{2}-dfrac{7y^3}{24}right)bigg|^2_0=\ \ \ =dfrac{137}{60}+dfrac{14}{3}=6{,}95$

Приложения:

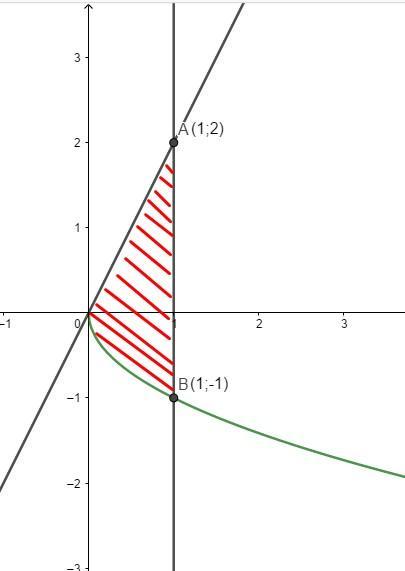
Ответил dnepr1

Вычислить двойной интеграл - значит найти число, равное площади фигуры D. Но по рисунку площадь (похожая на треугольник) примерно равна (1/2)*3*1 = 1,5. В ответе около 7. Есть сомнения в правильности ответа.

Ответил triggerbott

но подынтегральная функция есть по условию.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

помогите пожалуйста :з...

Русский язык, 1 год назад

ПРОЧИТАЙ ВНИМАТЕЛЬНО ПЕРВЫЙ АБЗАЦ И ПОДУМАЙ ,КАК НАИБОЛЕЕ КРАТКО ПЕРЕСКАЗАТЬ ЕГО.ЗАТЕМ ТАК ЖЕ ПЕРЕСКАЖИ ОСТАЛНЫЕ АБЗАЦЫ.ЗАПИШИ КРАТКОЕ ИЗЛОЖЕНИЕ ТЕКСТА.(ПОМОГИТЕ ПЛИЗЗЗЗЗЗЗЗЗЗЗЗ ЗАРАНЕЕ СПАСИБО.) ...

Биология, 7 лет назад

звуки голоса образуются при прохождении воздуха через ...

Литература, 7 лет назад

характеристика выскочки в рассказе "Выскочка" ПОМОГИТЕ ПЖ ДАМ 25 БАЛЛОВ...

Обществознание, 8 лет назад

сферы жизни общества (выбрать не верный ответ)...

История, 8 лет назад

Назовите полководца который участвовали в битве на реке Неве...