Алгебра, вопрос задал tihiyomutt , 1 год назад

Вычислить производную функции:

а) $x^{2} * tgx$

б) $y=\frac{2x-3}{x^{2} +1}$

в) $y=15x^{4} - 8x^{3} +5x^{2} - 7x+17$

Ответы на вопрос

Ответил elinakhilko

1

$1)\\x^{2} *tgx \\(u*v)^{'} = (u^{'} v*v^{'} u)\\ u=x^{2} \\u^{'} = 2x\\v=tgx\\v^{'} =\frac{1}{cos^{2}x } \\y^{'} =2x*tgx+\frac{1}{cos^{2}x } *x^{2} \\2) \\y=\frac{2x-3}{x^{2}+1} \\(\frac{u}{v})^{'} = \frac{u^{'}v-v^{'}u}{v^{2}}\\ u=2x+3\\u^{'} =2\\v=x^{2} +1\\v^{'} =2x\\y^{'} =\frac{2(x^{2}+1)-2x(2x+3)}{(x^{2}+1)^{2}} \\3)\\y^{'} = 60x^{3} -24x^{2} +10x-7$

tihiyomutt: Знать бы ещё, что такое /strong

elinakhilko: уже все хорошоюСайт выдал ошибку(

tihiyomutt: Хорошо, спасибо

tihiyomutt: Остальное можешь решить ?

tihiyomutt: Если не сложно :)

elinakhilko: Что остальное ?

tihiyomutt: А, лол

tihiyomutt: Я думал, что тут решение только под буквой а)

tihiyomutt: Спасибо огромное ;)

elinakhilko: Хахах,бывает)

Ответил Аноним

1

решение во вложении. там же ответы)

Приложения:

Предыдущий вопрос

Следующий вопрос

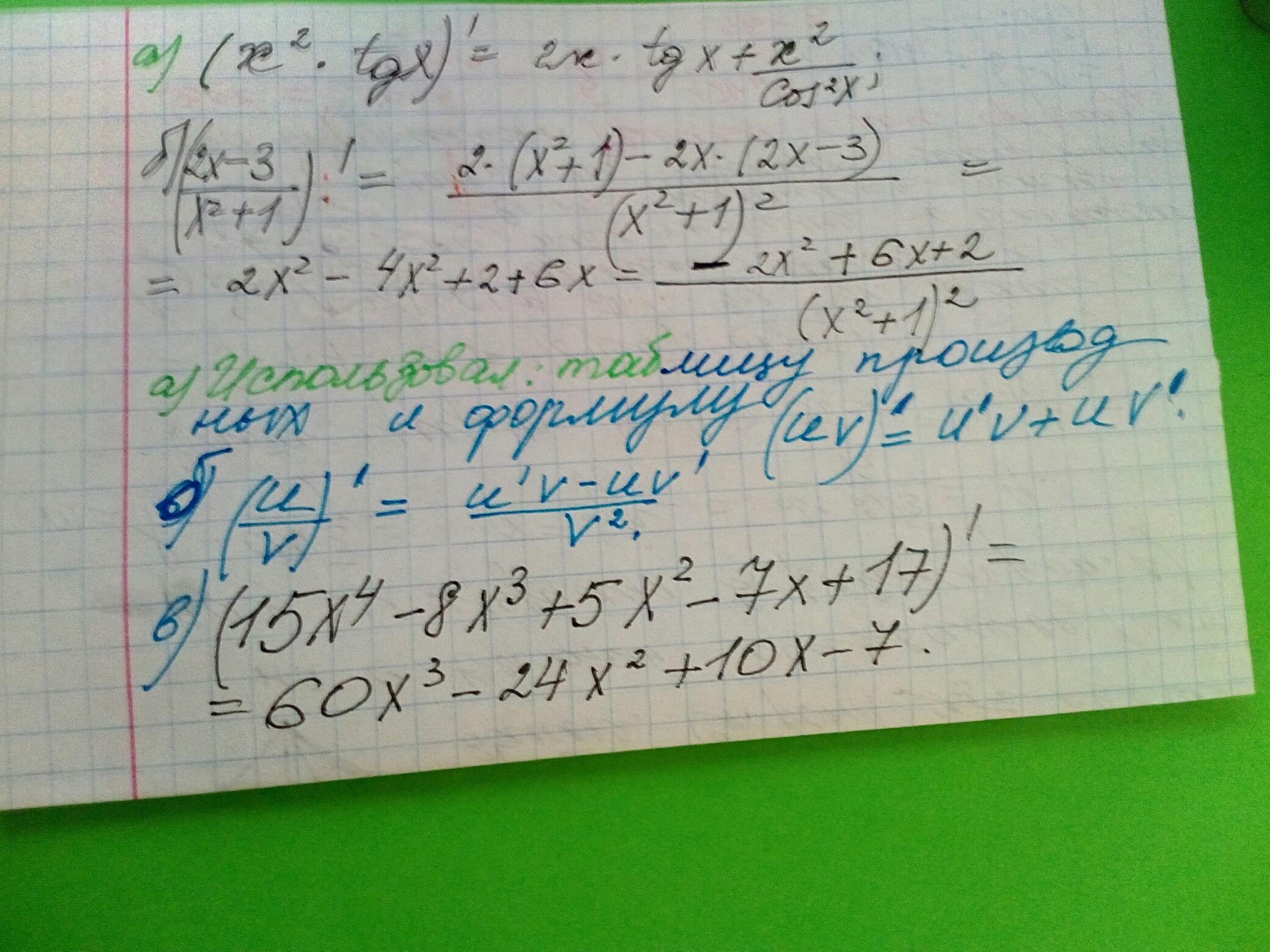
Новые вопросы

Геометрия, 1 год назад

допоможіть установити відповідність...

Музыка, 1 год назад

Розкажіть про історію виникнення рапсодії. Що означає поняття "Рарсодія"? Назвіть автора рапсодії, яку слухали...

Математика, 1 год назад

на доске 10 меньших чисел, каждое из которых содержит 2 или более. их сумма может быть равна 71...

Математика, 1 год назад

Помогите пожалуйста, срочно...

История, 6 лет назад

Помогите пожалуйста!СРОЧНО. 7 класс!

Математика, 6 лет назад

3x⁴-2x³+x² помогите 10 балов...