Математика, вопрос задал lowpunq , 1 год назад

Вычислить предел функции, используя 2-й замечательный предел. Задание на картинке.

Приложения:

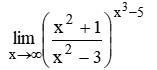
Ответы на вопрос

Ответил NNNLLL54

Ответ:

Второй замечательный предел : $\bf \lim\limits_{x \to \infty}\, \Big(1+\dfrac{1}{x}\Big)^{x}=\Big[\ 1^{\infty }\ \Big]=e$ .

$\bf \lim\limits _{x \to \infty}\Big(\dfrac{x^2+1}{x^2-3}\Big)^{x^3-5}=\lim\limits _{x \to \infty}\Big(\dfrac{x^2-3+3+1}{x^2-3}\Big)^{x^3-5}=\lim\limits _{x \to \infty}\Big(1+\dfrac{4}{x^2-3}\Big)^{x^3-5}=$

$\bf =\lim\limits _{x \to \infty}\left(\Big(1+\dfrac{4}{x^2-3}\Big)^{\frac{x^2-3}{4}}\right)^{\frac{4}{x^2-3}\cdot (x^3-5)}=e^{\lim\limits _{x \to \infty}\frac{4x^3-5}{x^2-3}}=\Big[\ e^{\infty }\ \Big]=\\\\\\=\left\{\begin{array}{l}\bf +\infty\ ,\ \ x\to +\infty \ ,\\\bf 0\ ,\ \ x\to -\infty \ .\end{array}\right$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 11 месяцев назад

Допоможіть будь ласка по алгебрі...

Алгебра, 11 месяцев назад

(5,6-4,5)³:0.1. помогите пж...

Биология, 1 год назад

висновок до повідомлення на тему: «Самшитова вогнівка її морфологічні та фізіологічні особливості та небезпека ураження самшиту та інших культур.» допоможііть...

Физика, 1 год назад

Грузовик движется влево, а самый правый след — это местоположение грузовика в момент t = 0. Временной интервал на графике трассировки составляет 2 секунды Какое местоположение будет у грузовика...

Химия, 6 лет назад

8 класс химия Свойства и соли 1)HCI 2)HF 3)HI 4) H2S 5)H2SO 6)H2SO3 7)HNO3 8)HNO2 9) H2CO3 10)H2SiO3 11)H3PO4 ПОМОГИТЕ ПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО!!! ДАЮ 20 БАЛОВ...

Химия, 6 лет назад

Помогите пожалуйста →фото←...