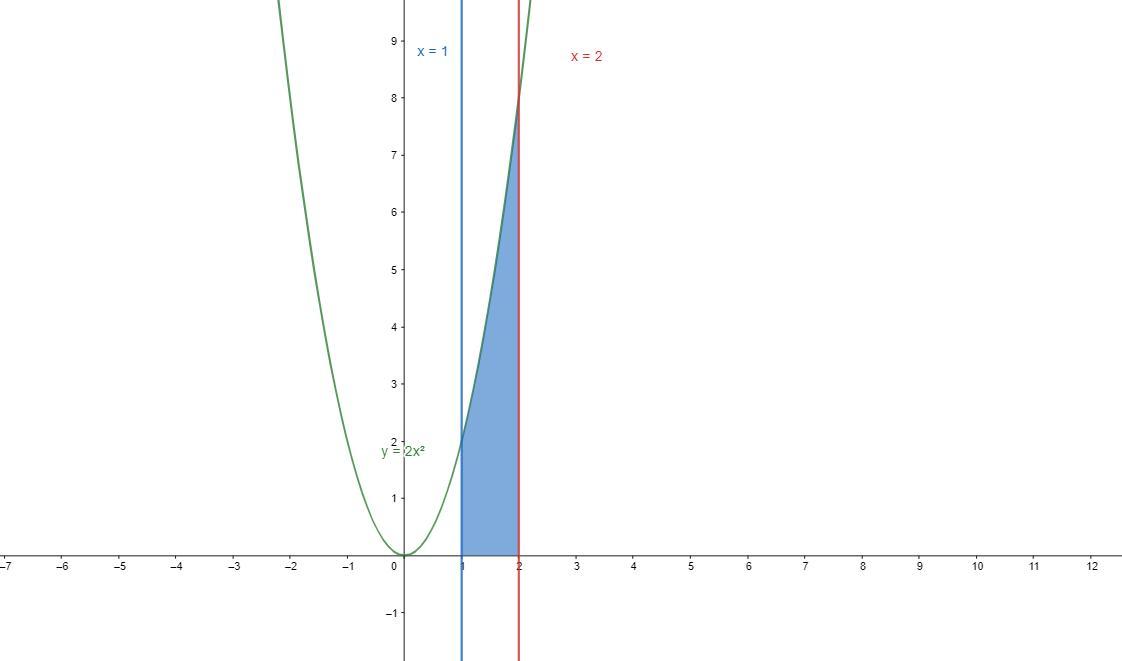
Алгебра, вопрос задал laurassa7114 , 1 год назад

вычислить площадь криволинейной трапеции ограниченной линиями срочно на бумажке сделайте и желательно понятно)

Приложения:

Ответы на вопрос

Ответил kamilmatematik100504

Ответ: $S = 4\dfrac{2}{3}$ (ед)²

Объяснение:

Находим определенный интеграл

$\displaystyle \int\limits^2_1 {2x^2} \, dx =\bigg(2\cdot\frac{x^{2+1}}{2+1} \bigg ) \Bigg |^2_1 =\bigg(\frac{2}{3}\cdot x^3 \bigg ) \Bigg |^2_1 =\frac{2}{3}\cdot 8 - \frac{2}{3} = \frac{14}{3} = 4\frac{2}{3}$

Приложения:

laurassa7114: Это вы точно номер 3 сделали?

kamilmatematik100504: Там нет 3-го номера , из условия " вычислить площадь криволинейной трапеции ограниченной линиям" получается нужно сделать только 6 номер .

laurassa7114: Аа да спасибо)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

помогите пожалуйста №1.Fill in the right form of “to be” and answer the questions. (Вставьте правильную форм у“to be” и ответьте на вопросы) My name ______ Pam. I _____ seven.I _____ from America. I...

Английский язык, 1 год назад

Просто перевод, пожалуйста...

Другие предметы, 1 год назад

прочитайте правила однієї з англійських шкіл, напишіть правила своєї школи) (напишіть правила для уроків англійської мови)...

Українська мова, 1 год назад

Скласти простий план до твору роздуму (чи потрібно здобувати освіту)...

Математика, 7 лет назад

реши уравнение (317,05-5х): 10,5+14,28=36,38...

География, 7 лет назад

по физикой карте полушария определите долготу городов Мехико Токио Каира ташкента и Москвы...