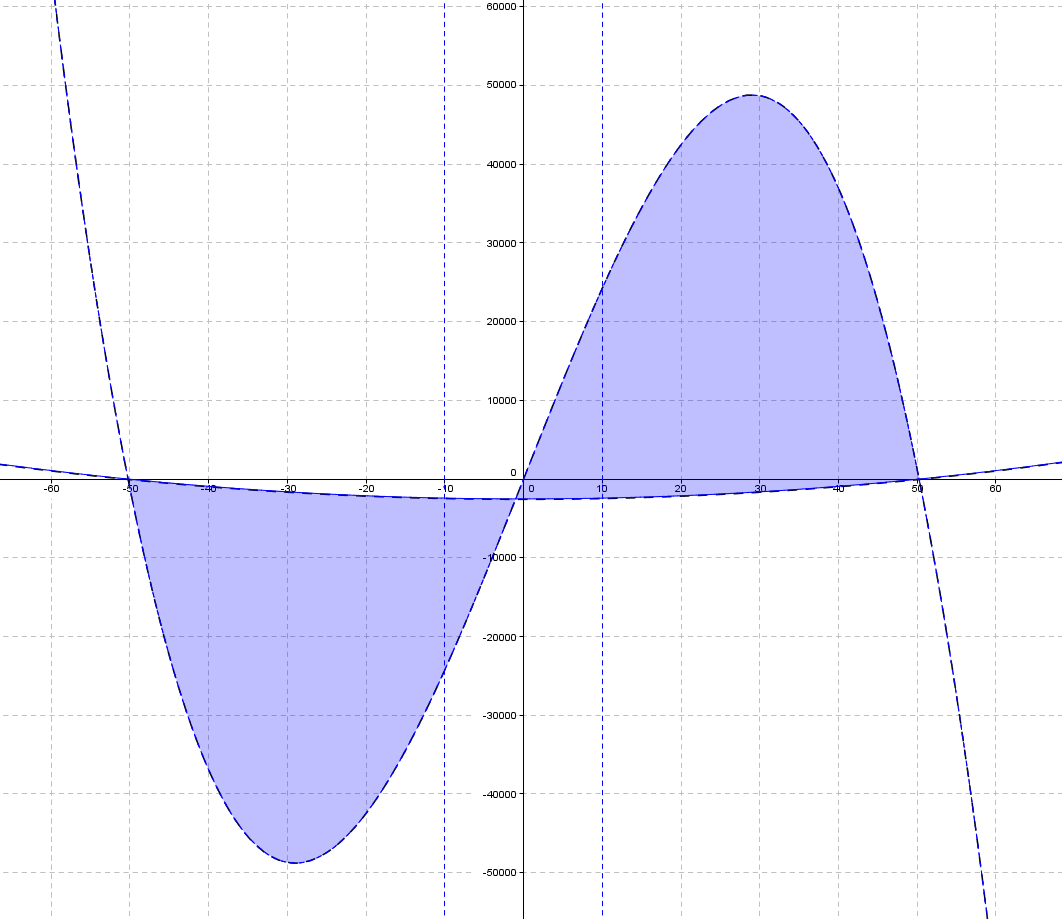
Вычислить площадь фигуры, пересеченной кривыми y=2523x-x^3, y=x^2-2523 и построить на плоскости данную фигуру
Ответы на вопрос
Ответил nelle987
0
Картинка во вложении.
Найдем точки пересечения:
2523x-x^3=x^2-2523
(x+1)(x^2-2523)=0
x=-1; x=+-sqrt(2523)
,dx=\=2intlimits_{1}^{sqrt{2523}}(x^3+x^2+2523x-2523),dx+intlimits_{-1}^1(x^2-2523),dx=](https://tex.z-dn.net/?f=displaystyle+S+%3D++intlimits%5E%7B-1%7D_%7B-sqrt%7B2523%7D%7D%28%28x%5E2-2523%29-%282523x-x%5E3%29%29%2Cdx-%5C-intlimits_%7B-1%7D%5E%7Bsqrt%7B2523%7D%7D%28%28x%5E2-2523%29-%282523x-x%5E3%29%29%2Cdx%3D%5C%3Dleft%5Bintlimits_%7B1%7D%5E%7Bsqrt%7B2523%7D%7D%2Bintlimits_%7B-1%7D%5E%7Bsqrt%7B2523%7D%7Dright%5D%28x%5E3%2Bx%5E2%2B2523x-2523%29%2Cdx%3D%5C%3D2intlimits_%7B1%7D%5E%7Bsqrt%7B2523%7D%7D%28x%5E3%2Bx%5E2%2B2523x-2523%29%2Cdx%2Bintlimits_%7B-1%7D%5E1%28x%5E2-2523%29%2Cdx%3D "displaystyle S = intlimits^{-1}_{-sqrt{2523}}((x^2-2523)-(2523x-x^3)),dx-\-intlimits_{-1}^{sqrt{2523}}((x^2-2523)-(2523x-x^3)),dx=\=left[intlimits_{1}^{sqrt{2523}}+intlimits_{-1}^{sqrt{2523}}right](x^3+x^2+2523x-2523),dx=\=2intlimits_{1}^{sqrt{2523}}(x^3+x^2+2523x-2523),dx+intlimits_{-1}^1(x^2-2523),dx=")
Найдем точки пересечения:
2523x-x^3=x^2-2523
(x+1)(x^2-2523)=0
x=-1; x=+-sqrt(2523)
Приложения:
Новые вопросы
Математика,
2 года назад
Математика,
2 года назад
Алгебра,
9 лет назад
Физика,
9 лет назад
Литература,
9 лет назад