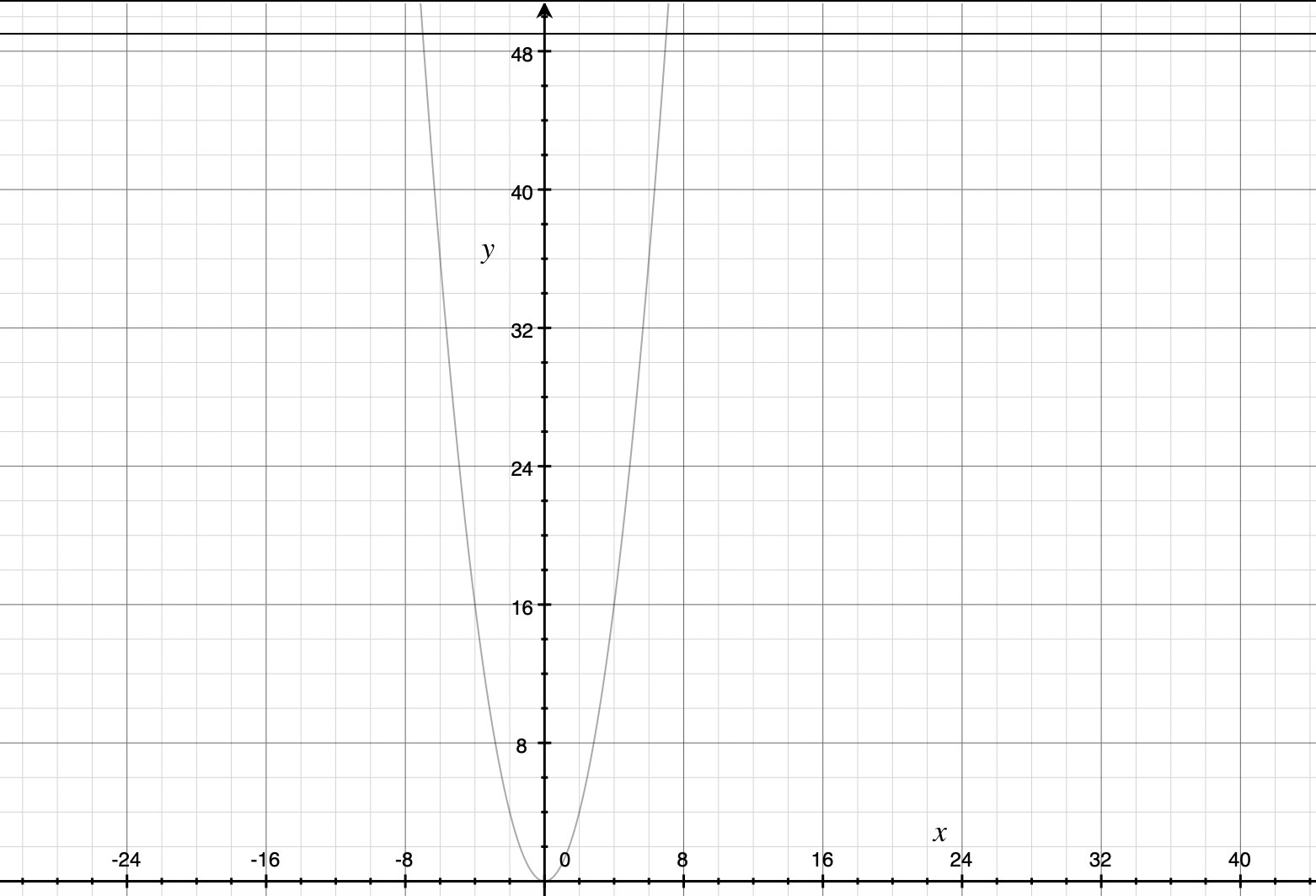
Вычислить площадь фигуры, ограниченную заданными линиями: a) y= x^2, y=49
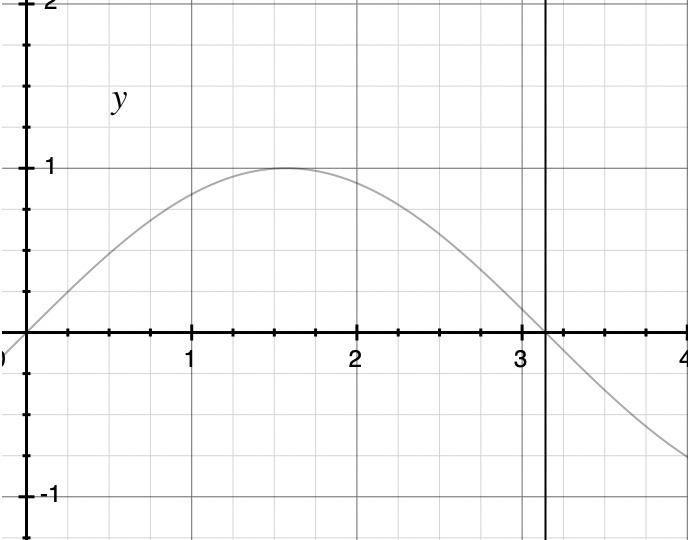
б) y=sin x , x=0, x=п
ЗАВТРА СДАВАТЬ ПОМОГИТЕ!!
ДАЮ 34 БАЛЛА
Приложения:

Ответы на вопрос
Ответил GTEgorss
0
а) Нам надо найти площадь фигуры на первой картинке
Находим иксы, от которого и до которого мы будем интегрировать, то есть находим точки пересечения параболы и прямой.
Решаем: x^2=49; x=±7
По формуле интеграла ограниченной фигуры сверху и снизу мы имеем, что S=(integral)limits^7_-7 (49-x^2dx) (из верхней вычитаем нижнюю)
Теперь находит первообразную этой фукнции и считаем по формуле Ньютона-Лейбница
49x-x^3/3 |^7_7 = (49*7-7^3/3) - (49*(-7)-(-7)^3/3) = 2*7^3*(1-1/3)=4*7^3/3
б) Нас интересует площадь под вторым графиком
Снова интеграл: (integral)limits^π_0 (sin(x)dx) = -cos(x)|^p_0 =
= -cos(p) + cos(0) = 1 + 1 = 2
Вот и всё))
Приложения:
Новые вопросы