Вычислить площадь фигуры ограниченной линиями у=2x^2-4;у=4 помогите пожалуйста даю 99 балов

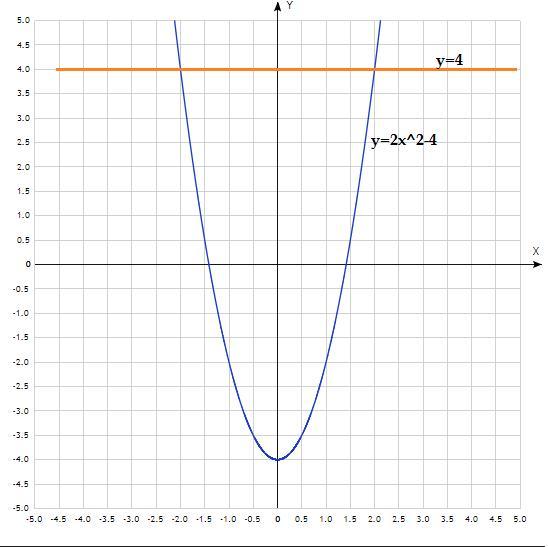
1) построим схематически графики y=2x²-4 и y=4

2) Найдем точки пересечения

2x²-4=4

2x²=8

x²=4

x=±2 это пределы интегрирования

Верхняя функция у=4, нижняя у=2x²-4