вычислить площадь фигуры ограниченного графика
Приложения:
Ответы на вопрос
Ответил xxxeol
0
ДАНО
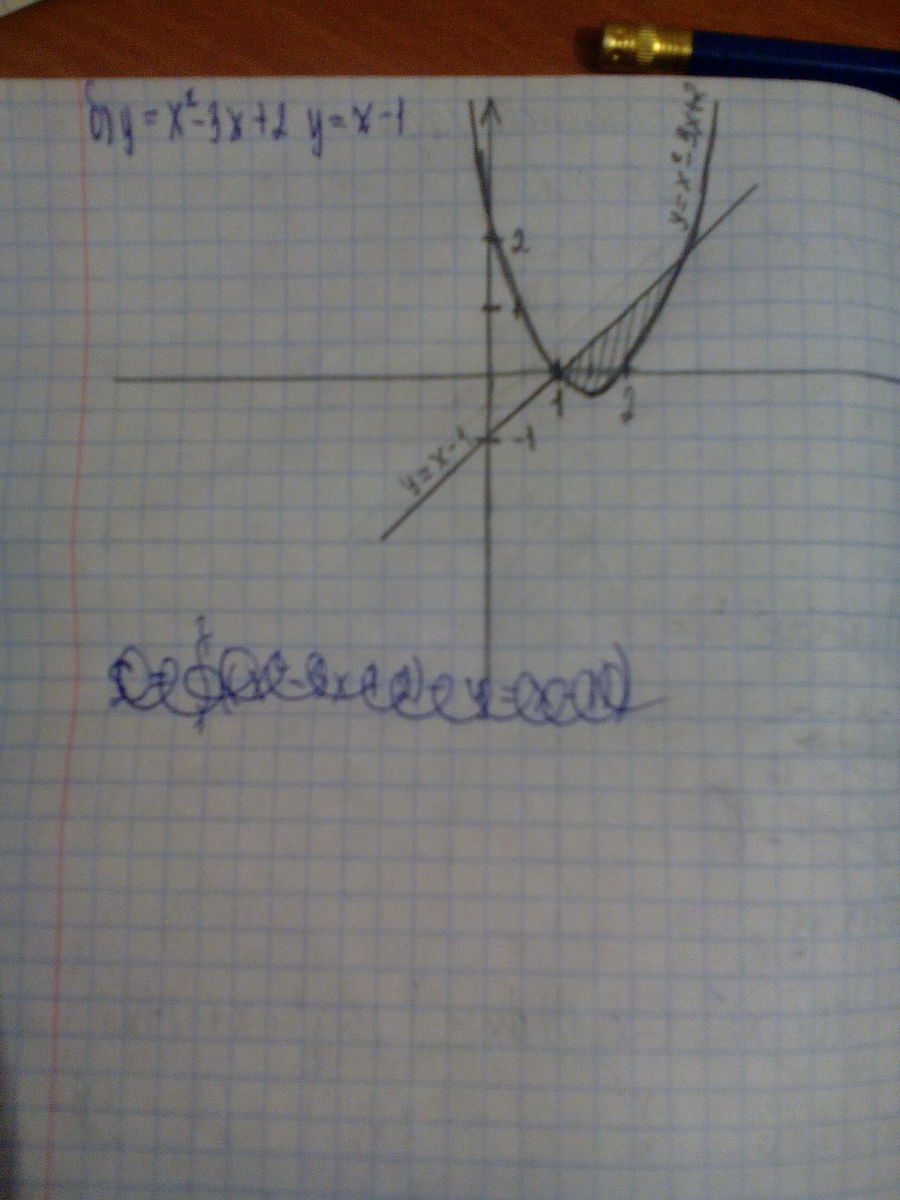
у1 = х² - 3х +2
у2 = х - 1
НАЙТИ
S=? - площадь фигуры.
РЕШЕНИЕ
1) Точки пересечения линий - решение квадратного уравнения
х² - 3х +х -1 =0. Корни x1 = 1 x2 = 3 - это пределы интегрирования.
2) Находим интегралы функций.
∫у1dx = 1/3*x³ - 3/2*x² +2*x + C
∫y2dx = 1/2*x² - x + C
Площадь фигуры равна разности площадей в пределах интегрирования от 1 до 3..
Вычисляем разность интегралов
1/3*(3³ - 1³) = 26/3 ~ 8 2/3
-4*(3² - 1²) = -16
3*(3 - 1) = 6
Итого площадь 16-6+8 2/3 = 1 1/3 - ОТВЕТ
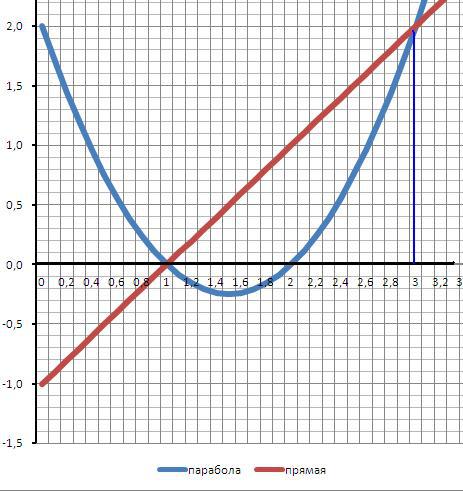
у1 = х² - 3х +2
у2 = х - 1
НАЙТИ
S=? - площадь фигуры.
РЕШЕНИЕ
1) Точки пересечения линий - решение квадратного уравнения
х² - 3х +х -1 =0. Корни x1 = 1 x2 = 3 - это пределы интегрирования.
2) Находим интегралы функций.
∫у1dx = 1/3*x³ - 3/2*x² +2*x + C
∫y2dx = 1/2*x² - x + C
Площадь фигуры равна разности площадей в пределах интегрирования от 1 до 3..
Вычисляем разность интегралов
1/3*(3³ - 1³) = 26/3 ~ 8 2/3
-4*(3² - 1²) = -16
3*(3 - 1) = 6
Итого площадь 16-6+8 2/3 = 1 1/3 - ОТВЕТ
Приложения:
Новые вопросы
Физкультура и спорт,
2 года назад
Биология,
2 года назад
Математика,
8 лет назад
Алгебра,
8 лет назад
История,
9 лет назад