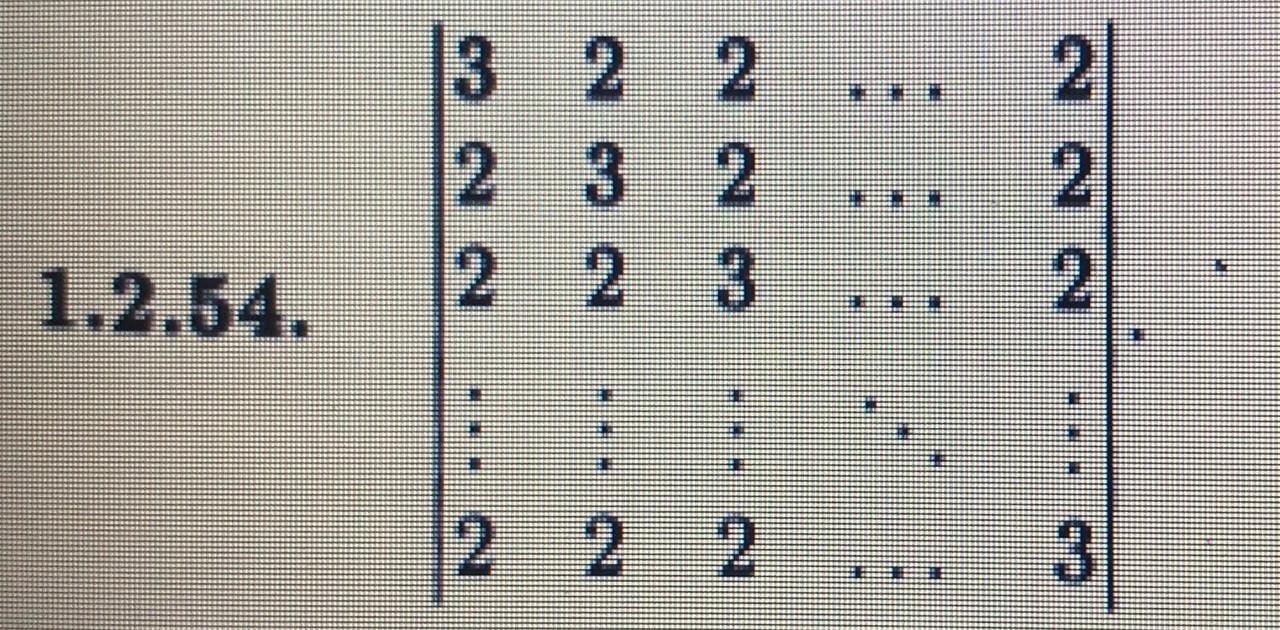
Алгебра, вопрос задал 2fzt2m5sy3 , 2 года назад

Вычислить определители n-го порядка

Приложения:

Ответы на вопрос

Ответил igorShap

Ответ:

$2n+1$

Объяснение:

(1) - отняли n-ую строку от каждой из остальных.

(2) - вычитаем из последней строки все остальные, домноженные на 2

(3) - разложим определитель по элементам n-ой строки

(4) - определитель единичной матрицы порядка n-1 равен 1 ∀n>1, n∈N.

$\begin{equation*}\left|\begin{array}{ccccc}3 & 2 & 2 & \ldots & 2\\2 & 3 & 2 & \ldots & 2\\ 2 & 2 & 3 & \ldots & 2\\\vdots & \vdots & \vdots & \ddots & \vdots\\2 & 2 & 2 & \ldots & 3\end{array}\right|\stackrel{=}{(1)}\left|\begin{array}{ccccc}1 & 0 & 0 & \ldots & -1\\0 & 1 & 0 & \ldots & -1\\ 0 & 0 & 1 & \ldots & -1\\\vdots & \vdots & \vdots & \ddots & \vdots\\2 & 2 & 2 & \ldots & 3\end{array}\right|\stackrel{=}{(2)}\end{equation*}$

$\begin{equation*}=\left|\begin{array}{ccccc}1 & 0 & 0 & \ldots & -1\\0 & 1 & 0 & \ldots & -1\\ 0 & 0 & 1 & \ldots & -1\\\vdots & \vdots & \vdots & \ddots & \vdots\\0 & 0 & 0 & \ldots & 3+2(n-1)\end{array}\right|\stackrel{=}{(3)}(3+2(n-1))\left|\begin{array}{ccccc}1 & 0 & 0 & \ldots & 0\\0 & 1 & 0 & \ldots & 0\\ 0 & 0 & 1 & \ldots & 0\\\vdots & \vdots & \vdots & \ddots & \vdots\\0 & 0 & 0 & \ldots & 1\end{array}\right|\stackrel{=}{(4)}\end{equation*}$