Вычислить определенный интеграл с помощью основных свойств и формулы Ньютона Лейбница
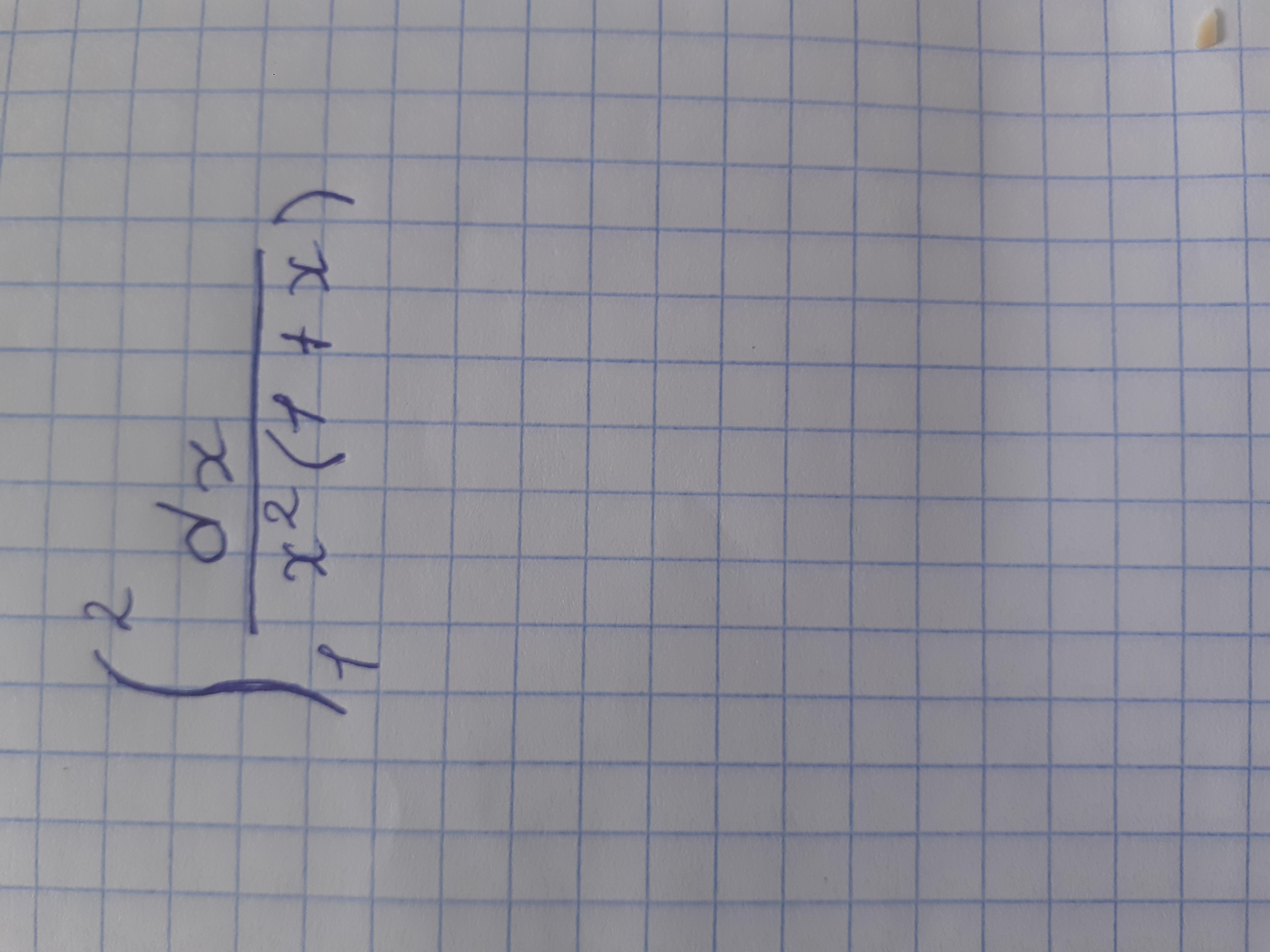
Ответы на вопрос
Ответ: I=1/2-2*ln(2)+ln(3)=1/2+ln(3/4).
Пошаговое объяснение:
Обозначим искомый интеграл через I. По формуле Ньютона-Лейбница, I=F(2)-F(1), где F(x)=∫dx/[x²*(1+x)]. В данном случае имеем дело с интегралом от рациональной дроби. Поскольку дробь - правильная, то 1/[x²*(1+x)]=(A*x+B)/x²+C/(1+x), где A, B и C - неизвестные пока коэффициенты. Приводя дроби справа к общему знаменателю и приравнивая затем числители дробей слева и справа, получаем уравнение 1=x²*(A+C)+x*(A+B)+B. Приравнивая теперь коэффициенты при одинаковых степенях x, получаем систему уравнений:
A+C=0
A+B=0
B=1
Решая её, находим A=-1, B=C=1. Отсюда 1/[x²*(1+x)]=(1-x)/x²+1/(1+x). Тогда F(x)=∫dx/[x²*(1*x)]=∫dx/x²-∫dx/x+∫d(1+x)/(1+x)=-1/x-ln/x/+ln/1+x/. Отсюда I=-1/2-ln(2)+ln(3)+1+ln(1)-ln(2)=1/2-2*ln(2)+ln(3)