Математика, вопрос задал nexellios , 1 год назад

Вычислить объем тела, образованного вращением плоской фигуры вокруг оси ох: y = 2/x; y = 0; xє[1;4]

Ответы на вопрос

Ответил FaerVator

Ответ:

3π (ед³)

Пошаговое объяснение:

Нас интересует 1-ая и 4-ая четверть системы координат.

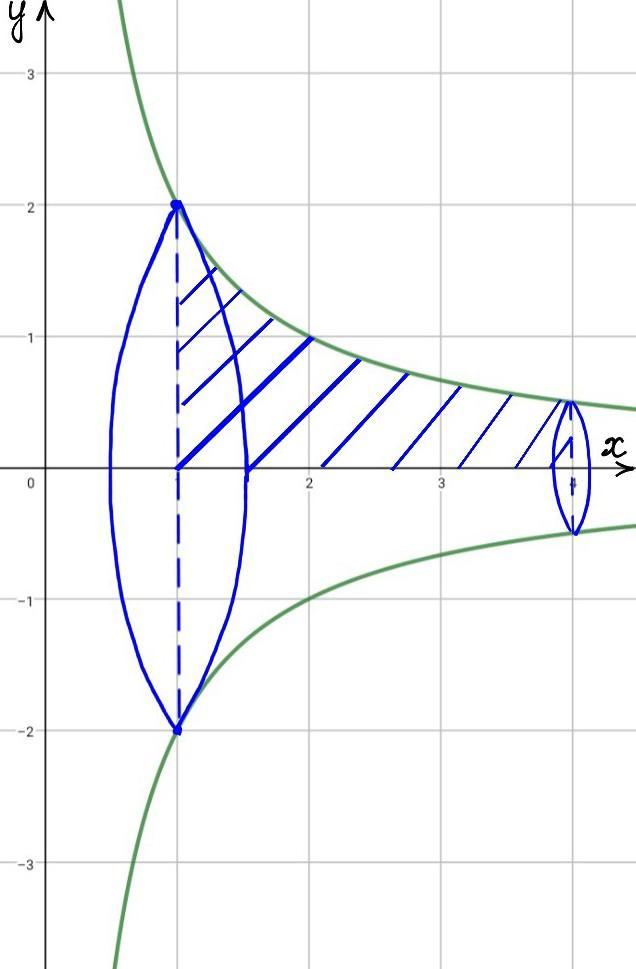
Строим график гиперболы.

$\displaystyle y = \frac{2}{x}$

Подберём точки.

При х=1 $\Rightarrow$ y=2

При х=2 $\Rightarrow$ y=1

При х=4 $\Rightarrow$ y=0,5

При х=0,5 $\Rightarrow$ y=4

(Строим симметричный график относительно оси Ох и далее все по фото)

Объём тела , полученного в результате вращения функции y=f(x) , ограниченной в промежутке [a;b] вокруг оси ох вычисляется по формуле:

$\boxed{ \boldsymbol{V=\pi \int ^b_af^2(x) d x} }$

По условию функция ограниченна в промежутке от 1 до 4 , находим объем:

$\displaystyle V=\pi \int ^4_1 \bigg( \frac{2}{x} \bigg) ^{2} d x = \pi \int ^4_1 \frac{4}{x {}^{2} } d x = \frac{ - 4\pi}{x} \bigg|^4_1 = - \pi - ( - 4 \pi) = 3 \pi(ed^3)$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Геометрия, 1 год назад

помогите пожалуйстаааааа Прямокутні трикутники, що зображені на малюнку, будуть рівними. Виберіть одну відповідь: За двома катетами За гіпотенузою і гострим кутом За катетом та прилеглим до...

Химия, 1 год назад

Прошу помогите. Даю 15 баллов Дати характеристику фізичних та хімічних властивостей одній простій та одній складній речовині (оксиду) на власний вибір...

Физика, 1 год назад

Помогите пожалуйста срочно. 3. Решите задачи: 1) По уравнению координаты x=4+5t-3t² определить: начальную координату, проекцию начальной скорости, проекцию ускорения. Написать уравнение скорости...

Алгебра, 1 год назад

Марина Павловна внимательно изучает цены в каталогах, прежде чем пойти за покупками. На сей раз она составила таблицу с ценами на продукты для выпечки из разных магазинов. Мука продаётся...

Алгебра, 6 лет назад

решите пожалуйста через дескреминант...

Литература, 6 лет назад

Развёрнутый ответ на проблемный вопрос. "Что важнее: верность царю или месть и достоинство." в Песне про царя Ивана Васильевича, молодогоопричника и удалого купца КФалашникава.