вычислить интеграл xIn(x+7)dx
очень срочно!!!
Приложения:
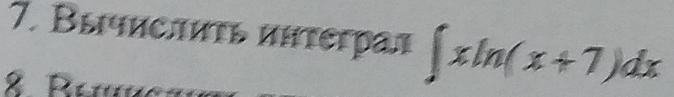
Ответы на вопрос
Ответил igorShap
0
Новые вопросы
Физика,
1 год назад
Қазақ тiлi,
1 год назад
Английский язык,
1 год назад
Математика,
1 год назад
Математика,
6 лет назад