Алгебра, вопрос задал RedBaron , 9 лет назад

Вычислить интеграл (с проверкой):
$intsqrt{2-x-x^{2}}$

Ответы на вопрос

Ответил bearcab

Воспользуемся формулой

$intsqrt{a^2-t^2}dt=frac{t}{2}sqrt{a^2-t^2}+frac{a^2}{2}arcsin(frac{t}{a})+C$

Теперь сам интеграл следует привести к этому виду

$intsqrt{2-x-x^2}dx=intsqrt{2+0,25-0,25-x-x^2}dx=$

$=intsqrt{2,25-(0,25+x+x^2)}dx=intsqrt{2,25-(0,5+x)^2)}dx=$

$=intsqrt{2,25-(0,5+x)^2)}d(x+0,5)$
Замена t=x+0,5.

$intsqrt{2,25-t^2}dt=intsqrt{1,5^2-t^2}dt=frac{t}{2}sqrt{2,25-t^2}+frac{2,25}{2}arcsinfrac{t}{1,5}+C$

Теперь подставим вместо t его значение (x+0,5).

$=frac{x+0,5}{2}sqrt{2,25-(x+0,5)^2}+frac{2,25}{2}arcsin(frac{x+0,5}{1,5})+C=$

$=frac{x+0,5}{2}sqrt{2-x-x^2}+frac{9}{8}arcsin(frac{2*(x+0,5)}{3})+C=$

$=frac{x+0,5}{2}sqrt{2-x-x^2}+frac{9}{8}arcsin(frac{2x+1}{3})+C=$

$=frac{2x+1}{4}sqrt{2-x-x^2}+frac{9}{8}arcsin(frac{2x+1}{3})+C=$

А проверку я напишу во вложении. Она сложная, лучше ее отсканированным файлом отправить.

Приложения:

Предыдущий вопрос

Следующий вопрос

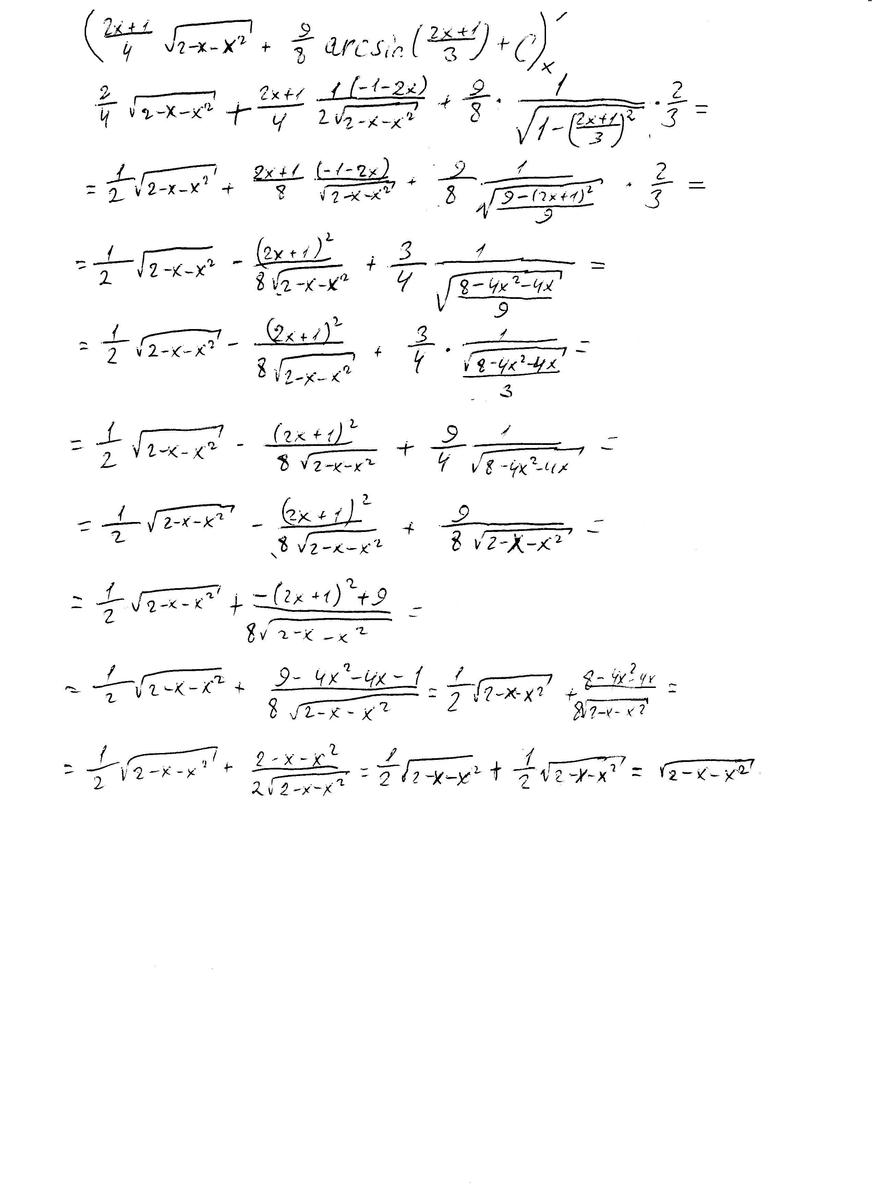
Новые вопросы

Геометрия, 2 года назад

знайдіть площу ромба якщо його діагоналі дорівнюють 8см і 11 см...

Физика, 2 года назад

Чому дорівнює момент сили , якщо сила дорівнює 5 Н, а плече дії сили 10 см ? *...

Математика, 9 лет назад

Число 54 уменьшить в 6 раз.На сколько едениц уменьшили 54?

Информатика, 9 лет назад

1. Какими средствами приема сигналов из внешнего мира обладает человек?

Математика, 9 лет назад

найти наименьшее общее кратное для чисел 35 7 10 5...

География, 9 лет назад

на каком расстоянии друг от друга находятся урал и поволжье???