Алгебра, вопрос задал ВладимирБ , 2 месяца назад

Вычислить.....................

Приложения:

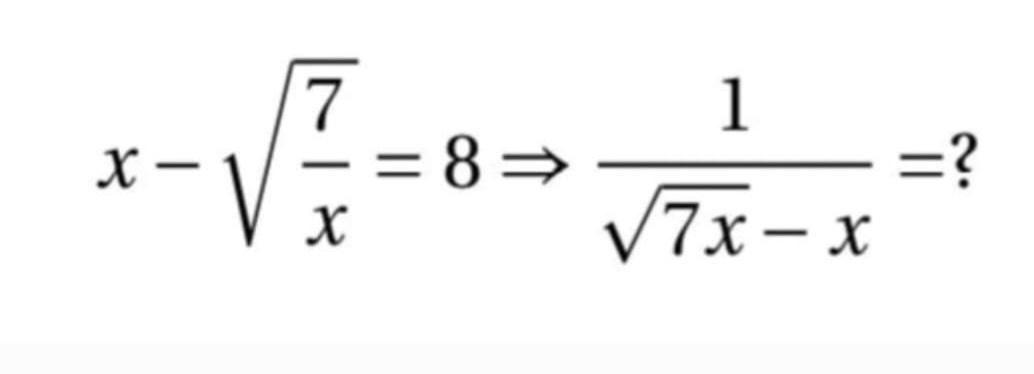
Ответы на вопрос

Ответил forqforq

Ответ:

-1

Объяснение:

1-ый "механический" способ.

Можно найти х из первого уравнения и попытаться подставить его во второе выражение, при этом аппроксимируя полученный результат (чаще всего ответом таких примеров является целое число).

$x-\sqrt{\frac{7}{x}} =8\\\sqrt{x}=t > 0\\t^2-\frac{\sqrt{7}}{t}=8\\t^3-8t-\sqrt{7}=0\\\sqrt{7}=p\\t^3-p^2t-t-p=0\\t(t^2-p^2)-(t+p)=0\\t(t-p)(t+p)-(t+p)=0\\(t+p)(t^2-tp-1)=0\\(t+\sqrt{7})(t^2-\sqrt{7}t-1)=0\\t_1=-\sqrt{7}\\t_2=\frac{\sqrt{7}+\sqrt{11}}{2}\\t_3=\frac{\sqrt{7}-\sqrt{11}}{2}\\\\$

t₁ и t₃ меньше 0, поэтому мы их сразу отбраковываем. Остается только t₂. Делаем обратную замену

$\sqrt{x}=\frac{\sqrt{7}+\sqrt{11}}{2} \\x=\sqrt{\frac{\sqrt{7}+\sqrt{11}}{2}}$

Подставляем полученное значение х во второе выражение и получаем страшное выражение:

$\frac{1}{\sqrt{7 \times\sqrt{\frac{\sqrt{7}+\sqrt{11}}{2}}}-\sqrt{\frac{\sqrt{7}+\sqrt{11}}{2}}} \\$

Приближенное вычисление через калькулятор дает примерно -1.

2-ой способ.

Преобразовываем второе выражение:

$\frac{1}{\sqrt{7x}-x} =\frac{1}{\sqrt{7x}-\sqrt{x}^2} =\frac{1}{\sqrt{x}(\sqrt{7}-\sqrt{x})}\ |\times\frac{\sqrt{7}+\sqrt{x}}{\sqrt{7}+\sqrt{x}} |=\frac{\sqrt{7}+\sqrt{x}}{\sqrt{x}} \times\frac{1}{7-x} =(\sqrt{\frac{7}{x}}+1 )\times \frac{1}{7-x}$

Немного преобразуем первое выражение:

$x-\sqrt{\frac{7}{x}}=8\\\sqrt{\frac{7}{x}}+1=x-7$

Подставляем в выражение, которое мы преобразовали ранее и получаем:

$\frac{x-7}{7-x}=\frac{x-7}{-(x-7)} =\fbox{-1}$

ГАЗ52: А ещё преобразовать в 1 способе последнее выражение?

forqforq: Там если идти чисто математически, то просто приходим ко второму методу. Я его привел лишь как один из способов "оценки" подобных заданий, ибо часто "решение в лоб" позволяет найти примерное решение, которое впоследствие может пригодиться, чтобы проверить конечный результат чистого алгебраического решения.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 2 месяца назад

. У неозначеній формі всі дієслова рядка: А) розбігтися, нагромадити, воркотати, вирізьбити Б) знехтувати, знайти, повірили, хилитися В) відпороти, випорскнув, бажає, зневажити Г) домагатися,...

Английский язык, 2 месяца назад

Срочнооо помогите пожалуйста дам много балов!

Физика, 2 месяца назад

Помогите срочно!!! ПРОШУ!!!

Українська мова, 2 месяца назад

Напиши про погоду завікном викиристовуючи якомога більше прикметників 3-4 речень...

Математика, 6 лет назад

Просмотри изображенные на рисунке предметы. Одинаковые ли у них объемы? Просмотри изображенные на рисунке предметы. Одинаковые ли у них объемы? Выполни сравнение и проверь свои предположения...

Информатика, 6 лет назад

помогите срочно пожалуйста...