Вычислить:
1)lg40+lg25=
2)log2(15)-log2(30)=
(надеюсь вы поняли почему в скобках)
_____________________________________________________________________
Решить уравнение:
1)log2(x)=log2(72)-log2(9)=
2)lgx=2lg7-3lg3+lg8=
3)log12(x^2-8x+16)=0
4)log2,2(x)-4log2(x)+3=0
5)log3(x-2)+log3(x+2)=log3(2x-1)
_________________________________________________________________________
Решите неравенство:
1)log8(4-2x)=>2
2)log0.4(12x+2)=>log0.4(10x+16)
__________________________________________________________________
Буду очень благодарна)))
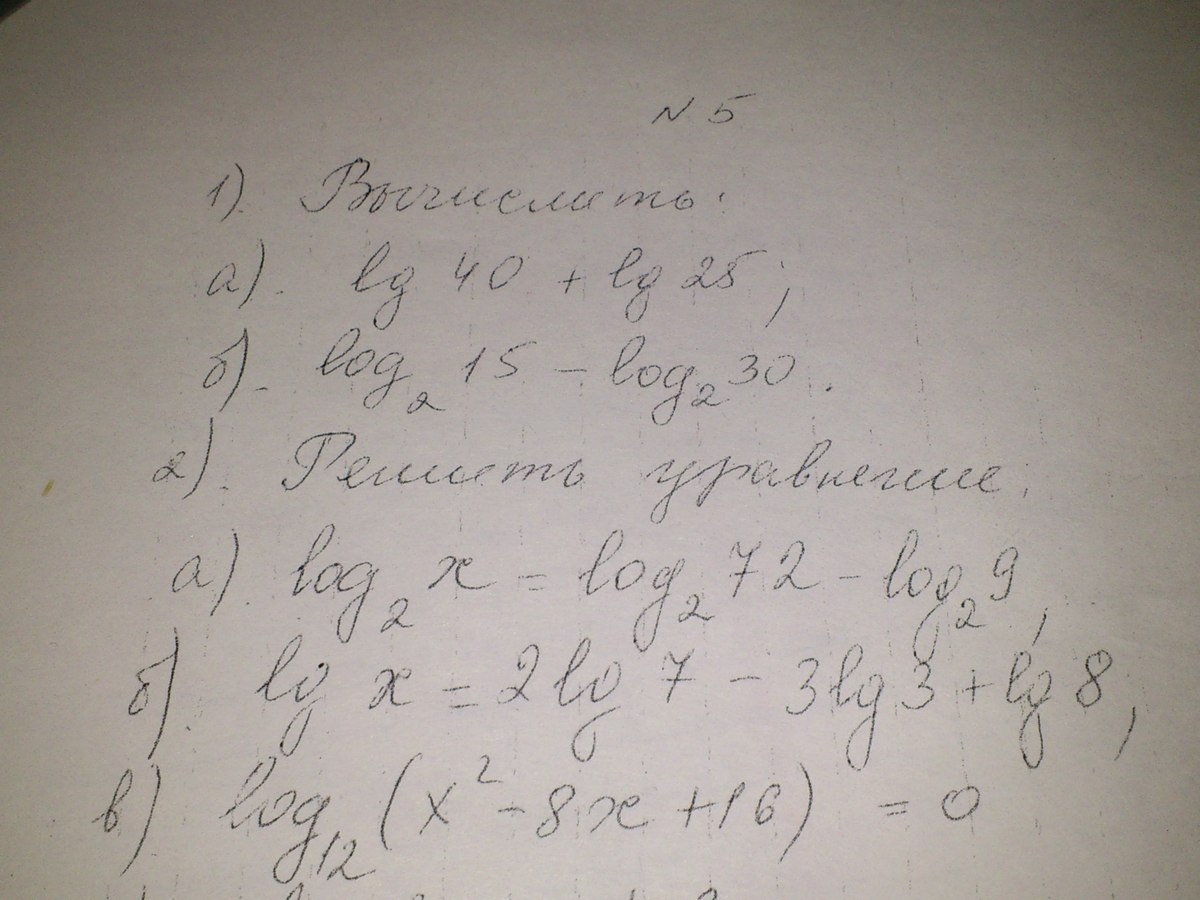
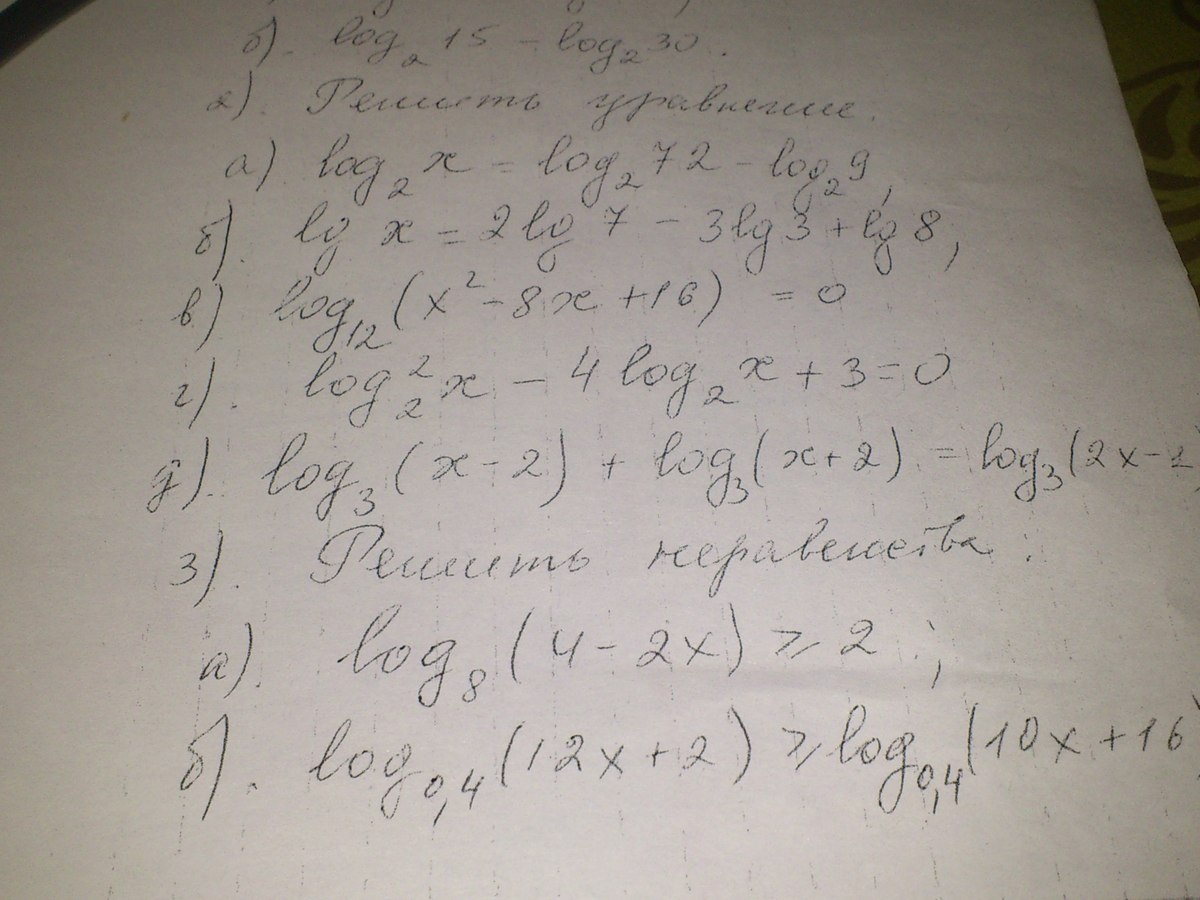
Ответы на вопрос
Вычислить:
1. lg(40*25)=lg1000=3
2. log2(15/30)=log2(2^-1)=-1
Решить уравнение:
1. log2(x)=log2(72/9)
log2(x)=log2(8)
log2(x)=3
x=2^3=8
2. lgx=lg(7^2/3^3*8)
lgx=lg(392/27)
x=392/27 (проверьте условие, вероятно, пропущена какая-то цифра)
3. x^2-8x+16=1
x^2-8x+15=0
D=64-60=4=2^2
x1=(8+2)/2=5, x2=(8-2)/2=3
4. пусть log2(x)=t, тогда
t^2-4t+3=0
D=16-12=4
t1=3, t2=1
log2(x)=3 или log2(x)=1
x=2^3=8 x=2^1=2
5. log3( (x-2)*(x+2)/(2x-1) )=0
(x^2-4)/(2x-1)=1
x^2-4=2x-1
x^2-2x-3=0
D=4+12=16
x1=3,
x2=-1 (посторонний корень, т.к. по области определения x>2)
Решите неравенство:
1. решим систему неравенств:
4-2x>0 и 4-2x=>64
x<2 и x=<30
таким образом, x принадлежит от (-бесконечности; 2)
2. по области определения x>-8/5
дальше решаем неравенство:
log0.4( (12x+2)/(10x+16) )=>0
(12x+2)/(10x+16)=>1
( (12x+2)-10x-16 )/(10x+16)=>0
(2x-14)/(10x+16)=>0
x=7 x не равно -8/5
методом интервалов приходим к выводу, что
х принадлежит от [7 до бесконечности)