вычисли угол между двумя касательными к окружности, если расстояние от его вершины до окружности равно радиусу окружности.
Ответы на вопрос
Ответил таня90
0
Дано:
окружность с центром О
АВ и ВС - касательные
ОА=ОС=МО=R
ВМ=МО
ВО=2R
_______________
∠АВС-?
АВ=ВС
OB - общая сторона→
Δ АВО=Δ СВО
∠С=∠А=90°
→Δ ОВС - прямоугольный
ОС=R, OB=2R - по условию
ОС - катет , ОС=1/2 гипотенузы ОВ→
∠ОВС=∠ОВА=30°
∠АВС=30*2=60°
окружность с центром О
АВ и ВС - касательные
ОА=ОС=МО=R
ВМ=МО
ВО=2R
_______________
∠АВС-?
АВ=ВС
OB - общая сторона→
Δ АВО=Δ СВО
∠С=∠А=90°
→Δ ОВС - прямоугольный
ОС=R, OB=2R - по условию
ОС - катет , ОС=1/2 гипотенузы ОВ→
∠ОВС=∠ОВА=30°
∠АВС=30*2=60°
Приложения:
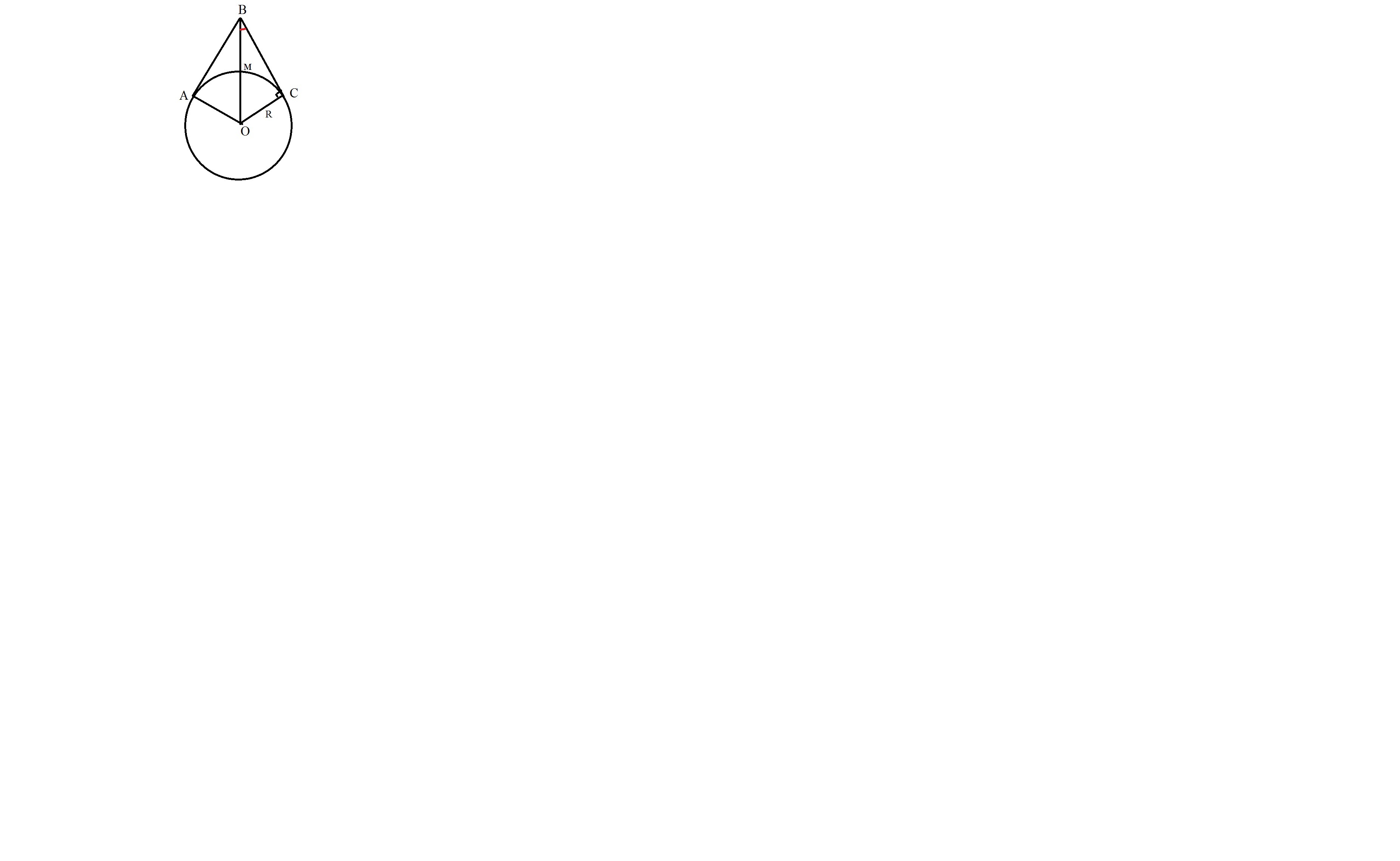
Новые вопросы