Вычеслите предел последовательности
Приложения:
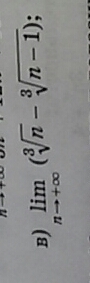
Ответы на вопрос
Ответил Alexandr130398
0
понадобиться формула разности кубов:
a³-b³=(a-b)(a²+ab+b²)
в нашем случае
а=∛n
b=∛(n-1)
Чтобы избавиться от неопределенности вида {∞-∞}, домножим числитель на выражение, чтобы получилась разность кубов и сразу же разделим на это выражение, чтобы результат не изменился
![lim_{n to infty} ( sqrt[3]{n} - sqrt[3]{n-1} )={ infty-infty}= \ \ lim_{n to infty} frac{( sqrt[3]{n} - sqrt[3]{n-1} )( sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2})}{( sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2})}= \ \ lim_{n to infty} frac{(sqrt[3]{n} )^3- (sqrt[3]{n-1})^3}{( sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2})} = \ \](https://tex.z-dn.net/?f=+lim_%7Bn+to+infty%7D+%28+sqrt%5B3%5D%7Bn%7D+-+sqrt%5B3%5D%7Bn-1%7D+%29%3D%7B+infty-infty%7D%3D++%5C++%5C+lim_%7Bn+to+infty%7D++frac%7B%28+sqrt%5B3%5D%7Bn%7D+-+sqrt%5B3%5D%7Bn-1%7D+%29%28+sqrt%5B3%5D%7Bn%5E2%7D+%2Bsqrt%5B3%5D%7Bn%7D+%2A+sqrt%5B3%5D%7Bn-1%7D+%2Bsqrt%5B3%5D%7B%28n-1%29%5E2%7D%29%7D%7B%28+sqrt%5B3%5D%7Bn%5E2%7D+%2Bsqrt%5B3%5D%7Bn%7D+%2A+sqrt%5B3%5D%7Bn-1%7D+%2Bsqrt%5B3%5D%7B%28n-1%29%5E2%7D%29%7D%3D+%5C++%5C++lim_%7Bn+to+infty%7D++frac%7B%28sqrt%5B3%5D%7Bn%7D+%29%5E3-+%28sqrt%5B3%5D%7Bn-1%7D%29%5E3%7D%7B%28+sqrt%5B3%5D%7Bn%5E2%7D+%2Bsqrt%5B3%5D%7Bn%7D+%2A+sqrt%5B3%5D%7Bn-1%7D+%2Bsqrt%5B3%5D%7B%28n-1%29%5E2%7D%29%7D+%3D+%5C++%5C+ "lim_{n to infty} ( sqrt[3]{n} - sqrt[3]{n-1} )={ infty-infty}= \ \ lim_{n to infty} frac{( sqrt[3]{n} - sqrt[3]{n-1} )( sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2})}{( sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2})}= \ \ lim_{n to infty} frac{(sqrt[3]{n} )^3- (sqrt[3]{n-1})^3}{( sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2})} = \ \")
![lim_{n to infty} frac{n-n+1}{ sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2}} = lim_{n to infty} frac{1}{sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2}} = \ \ = frac{1}{infty} =0](https://tex.z-dn.net/?f=+lim_%7Bn+to+infty%7D++frac%7Bn-n%2B1%7D%7B+sqrt%5B3%5D%7Bn%5E2%7D+%2Bsqrt%5B3%5D%7Bn%7D+%2A+sqrt%5B3%5D%7Bn-1%7D+%2Bsqrt%5B3%5D%7B%28n-1%29%5E2%7D%7D+%3D+lim_%7Bn+to+infty%7D++frac%7B1%7D%7Bsqrt%5B3%5D%7Bn%5E2%7D+%2Bsqrt%5B3%5D%7Bn%7D+%2A+sqrt%5B3%5D%7Bn-1%7D+%2Bsqrt%5B3%5D%7B%28n-1%29%5E2%7D%7D+%3D++%5C++%5C+%3D+frac%7B1%7D%7Binfty%7D+%3D0 "lim_{n to infty} frac{n-n+1}{ sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2}} = lim_{n to infty} frac{1}{sqrt[3]{n^2} +sqrt[3]{n} * sqrt[3]{n-1} +sqrt[3]{(n-1)^2}} = \ \ = frac{1}{infty} =0")
a³-b³=(a-b)(a²+ab+b²)
в нашем случае
а=∛n
b=∛(n-1)
Чтобы избавиться от неопределенности вида {∞-∞}, домножим числитель на выражение, чтобы получилась разность кубов и сразу же разделим на это выражение, чтобы результат не изменился
Новые вопросы