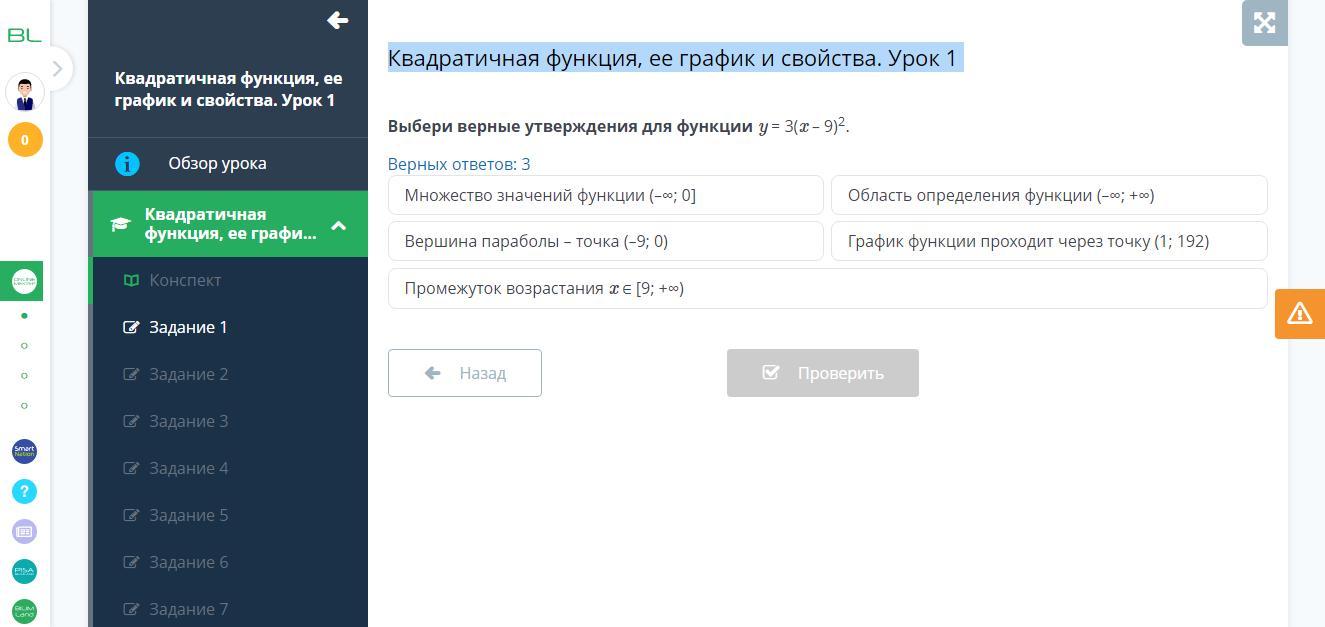
Выбери верные утверждения для функции y = 3(x – 9)2.
Ответы на вопрос
Ответ:
Область определения функции (-∞ ; + ∞ )
График функции проходит через точку (1 ; 192)
Промежуток возрастания
Объяснение:
№1
Найдем область значений функции
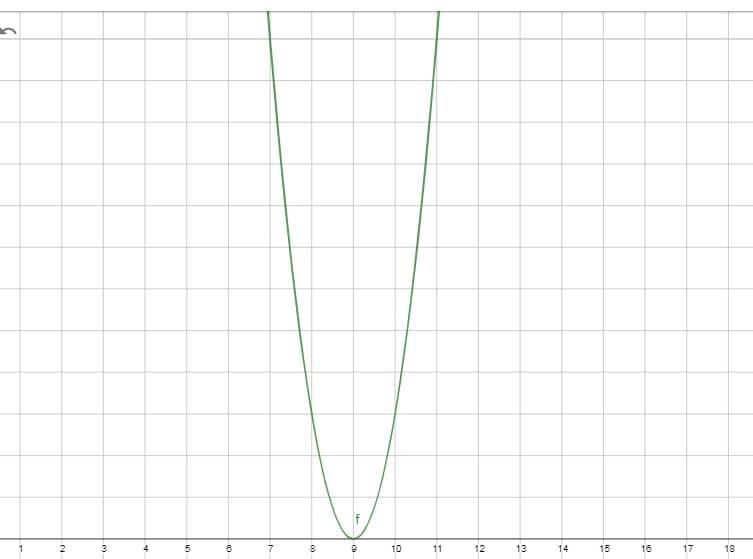
Найдем координаты вершины параболы
Тогда
В ответе сказано что
Это неверно
№2
Область определения любой квадратичной функции
(-∞ ; + ∞ ) верно
№3
Координаты вершины мы уже нашли
В ответе сказано что ее координаты (-9 ; 0) ,
что неверно
№4
Координаты точки (1 ; 192)
Подставим координаты в функцию
Верно функция проходит через точку (1 ; 192)
№5
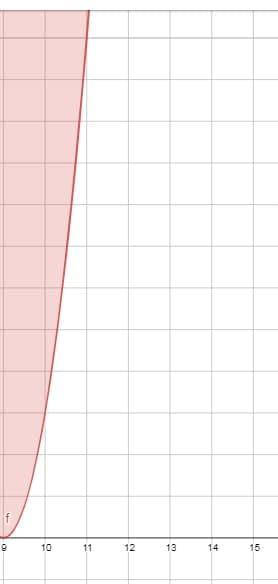
Найдем промежуток возрастания функции
Ветви параболы направлены вверх
Вершина параболы находиться в точке (9 ; 0)
Тогда промежуток начинается с точки 9 и идет до бесконечности
Графики в прикрепленном файле ; область выделенная красным и есть ответ
Тогда ответ верный