Все плоские углы при вершине треугольной пирамиды равны 45 град. Определить двугранные углы при её боковых ребрах
Ответы на вопрос
Ответил potapov19461
0
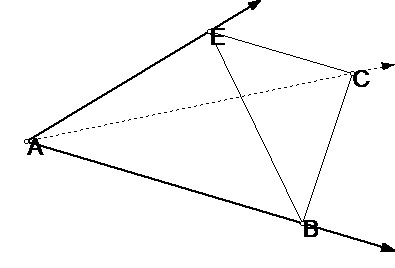
Пусть да н трехгранный угол А,где плоские углы равны по 45 градусов. Проведем через Е плоскость , перпендикулярно лучу АЕ. Получим линейный угол ВЕС.
Пусть АЕ-а, тогда ВЕ=СЕ=а. АВ=АС=а√2, по теореме Пифагора.
ВС²=АВ²+АС²-2*АВ*АС*cos45° = 2a²+2a²-2*2a²*√2/2=4a²-2a²√2 .
СоsВЕС=(ВЕ²+ЕС²-ВС²)/(2ВЕ*ЕС)= (а²+а²-(4a²-2a²√2))/2а²)=√2-1.
∠ВЕС= arccos(√2-1) ≈65°30'.
Остальные углы (при других ребрах) будут такие же.
Пусть АЕ-а, тогда ВЕ=СЕ=а. АВ=АС=а√2, по теореме Пифагора.
ВС²=АВ²+АС²-2*АВ*АС*cos45° = 2a²+2a²-2*2a²*√2/2=4a²-2a²√2 .
СоsВЕС=(ВЕ²+ЕС²-ВС²)/(2ВЕ*ЕС)= (а²+а²-(4a²-2a²√2))/2а²)=√2-1.
∠ВЕС= arccos(√2-1) ≈65°30'.
Остальные углы (при других ребрах) будут такие же.
Приложения:
Новые вопросы