Вписанная и вневписанная окружность треугольника ABC касаются стороны BC в точках P и Q. Вневписанные окружности треугольника ABC касаются продолжений стороны BC за точки B и C в точках X и Y. Найдите расстояние между серединами отрезков PQ и XY, если BC=24
Ответы на вопрос
Ответил antonovm
0
Ответ:
0 ( отрезки имеют общую середину )
Объяснение:
Доказал 2 вспомогательных утверждения , на олимпиадах их доказательство не обязательно
Приложения:
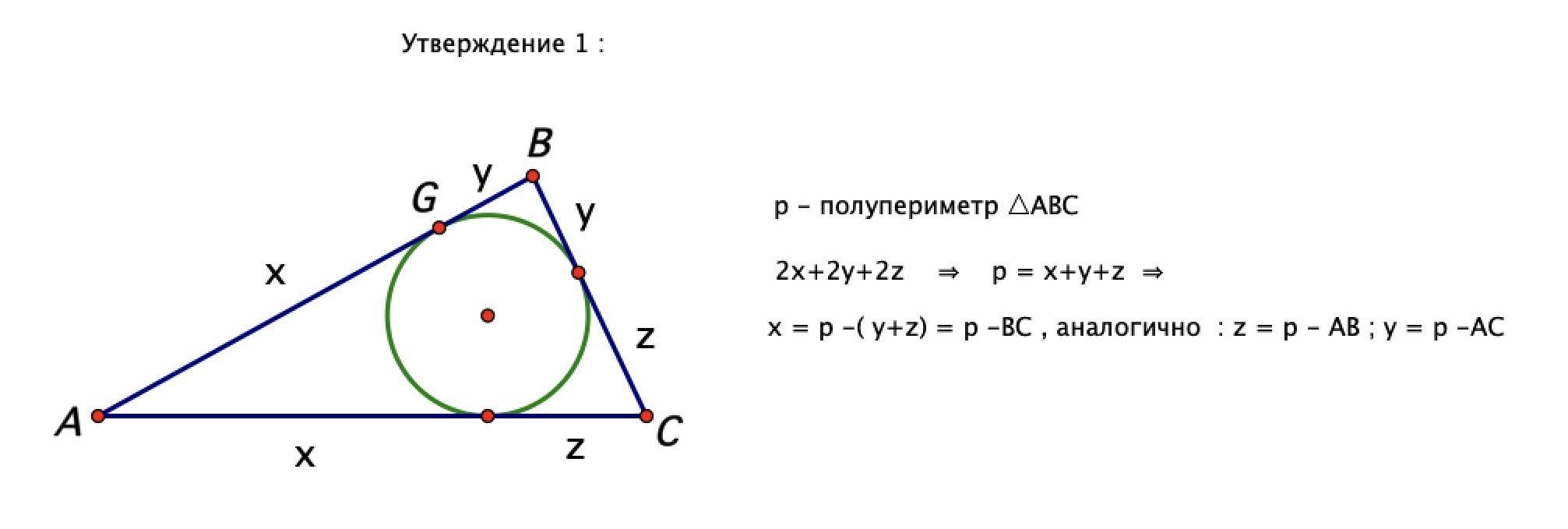
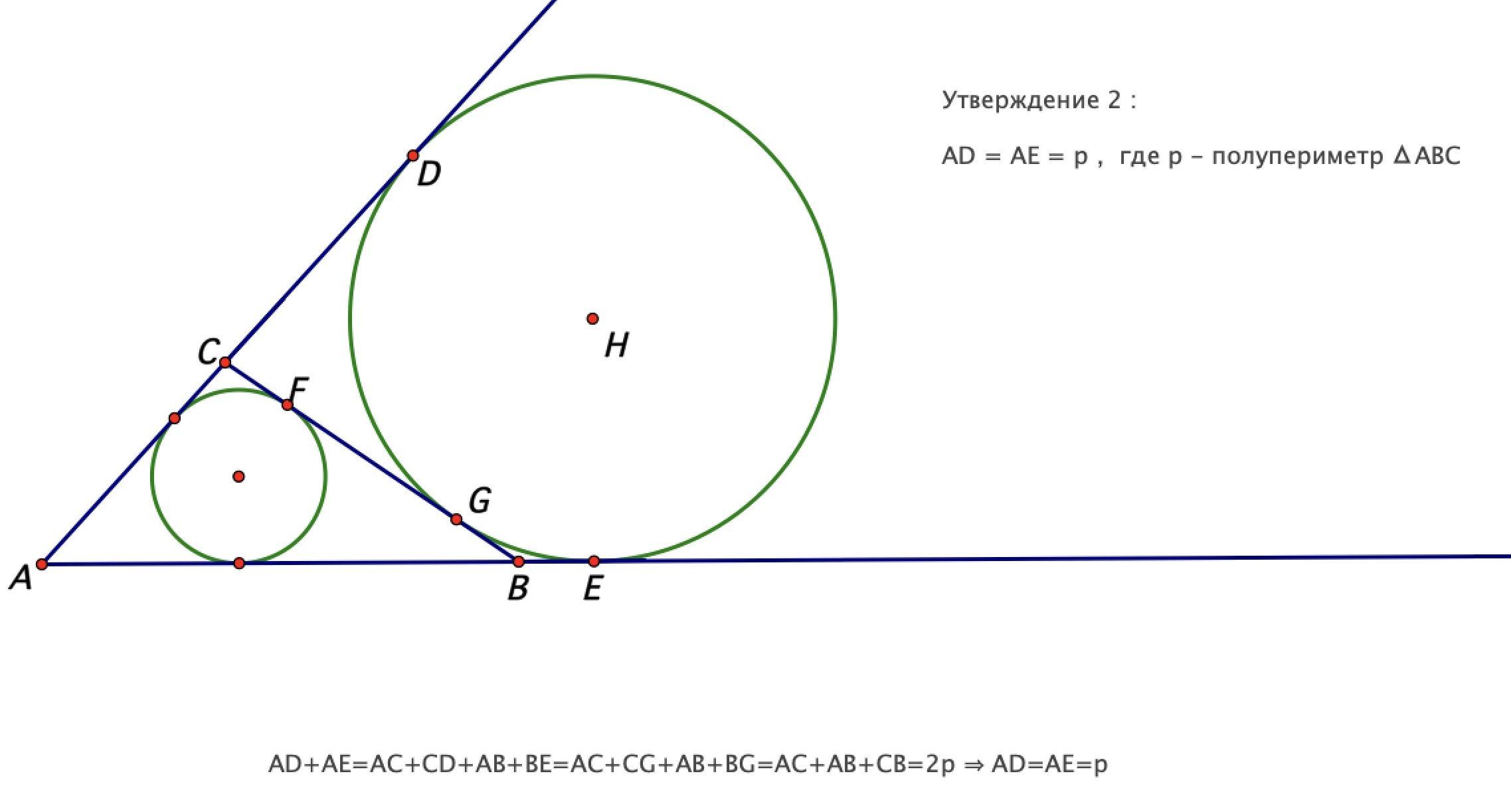
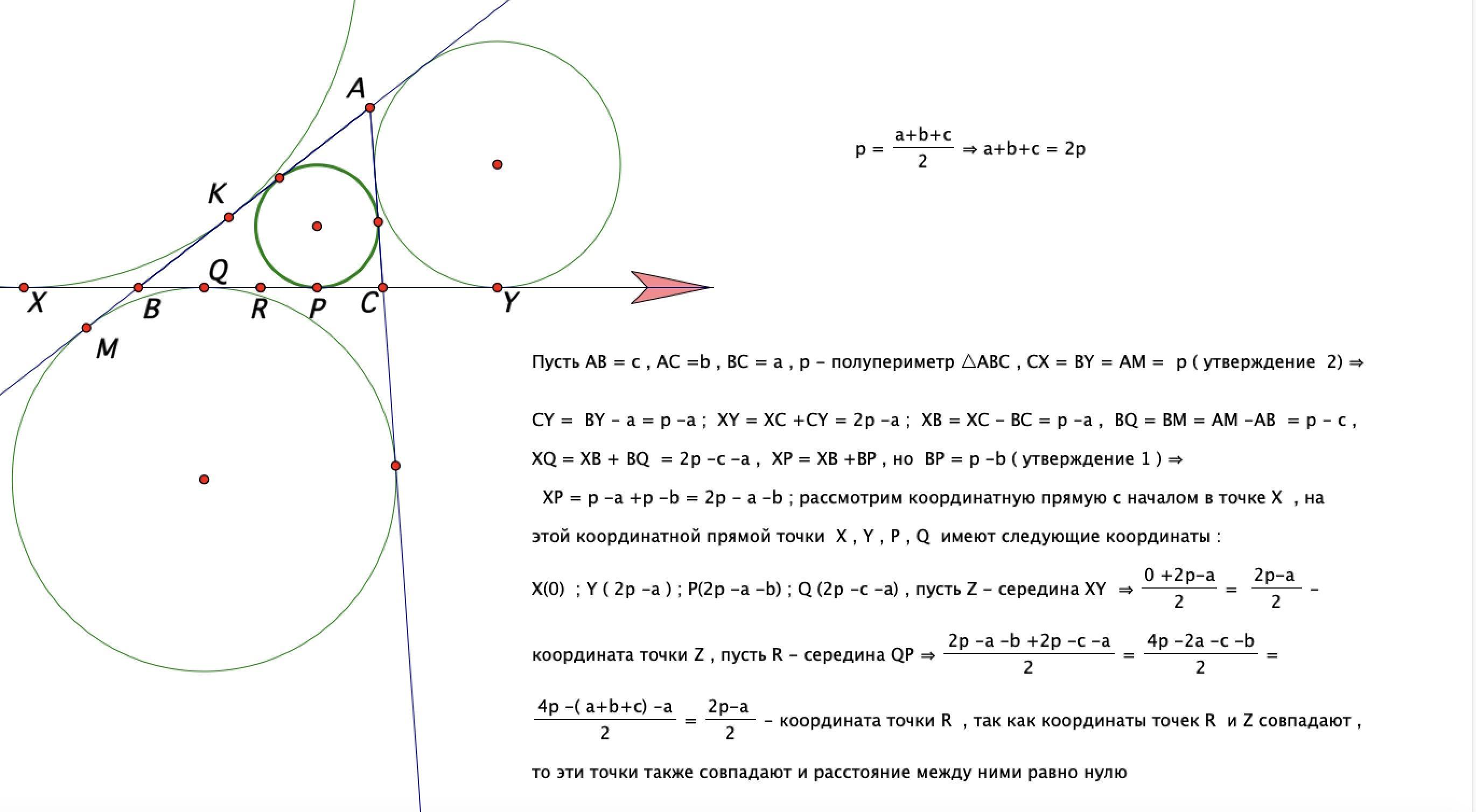
Ответил temasir15
0
Да, спасибо, все правильно
Ответил cos20093
0
Я уже где-то писал про эту задачу 1) Из вашего рисунка 2 легко вывести свойство общих касательных CF = BE; (кстати, "психологически" это равенство очень тяжело принимается) 2) для вписанных и вневписанных окружностей отсюда следует, что точки касания с одной из сторон симметричны относительно середины стороны. QR = RP
Ответил cos20093
0
3) цепочка равенств на основе того же свойства XB = BK =(1)= AK1 = AN =(1)= CY1 = CY, и точки X и Y тоже симметричны (точки K1 N и Y1 у вас не обозначены, но там понятно. K1- точка касания вписанной окружности с AB, N - с AC, Y1 - точка касания вневписанной окружности с AC. (1) означает применение свойства 1) ). Так решение не перегружено.
Ответил cos20093
0
Вы выводите хорошие, полезные и правильные соотношения для отрезков, но в этой задаче они не нужны.
Ответил cos20093
0
X и Y симметричны относительно R, конечно, сорри, пропустил часть фразы.
Новые вопросы