Вопрос по простым тригонометрическим уравнениям.
Когда в тригонометрическом уравнении к степени ставится +1
(пример подчеркнула на картинке)

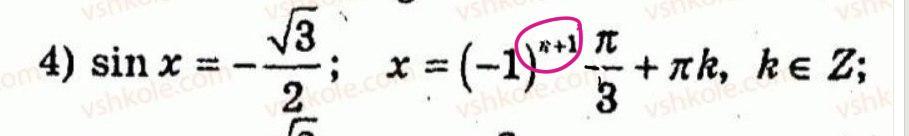
Vector91: Когда в правой части отрицательное число

Vector91: Оттуда и дополнительная -1

LFP: свойство функции арксинус: arcsin(-1/2) = -arcsin(1/2) = -1*arcsin(1/2)... и если есть еще один множитель (-1)^k*(-1)*arcsin(1/2), то при умножении (основания одинаковые -1) показатели степени складываются... (-1)^k*(-1)=(-1)^(k+1) т.е. Ответ: когда в уравнении синус равен отрицательному числу