Вокруг четырехугольника ABCD со сторонами АВ = 3 и DC = V6, описана окружность. Диагонали АC и BD пересекаются в точке Е. Найдите отношение BE : ED, если АЕ относится к ЕС как 3:2
Ответы на вопрос
Ответил nafanya2014
0
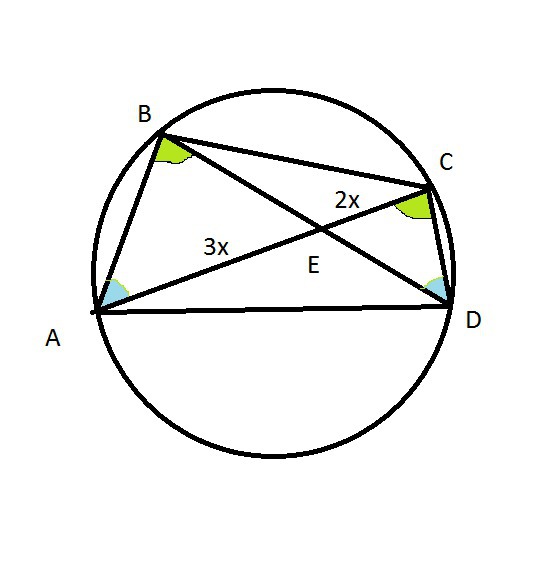
Вписанные углы, опирающиеся на одну и ту же дугу равны.
Такие углы отмечены на рисунке одинаковым цветом.
Треугольники АВЕ и CDE подобны по двум углам.
Из подобия следует отношение сторон:
АВ:CD = AE:ED ⇒ ED=CD·AE/AB=3x√6/3=x√6
AB:CD=BE:EC ⇒BE=x√6
BE:ED=x√6:(x√6)=1:1
О т в е т. BE:ED=1:1.
Такие углы отмечены на рисунке одинаковым цветом.
Треугольники АВЕ и CDE подобны по двум углам.
Из подобия следует отношение сторон:
АВ:CD = AE:ED ⇒ ED=CD·AE/AB=3x√6/3=x√6
AB:CD=BE:EC ⇒BE=x√6
BE:ED=x√6:(x√6)=1:1
О т в е т. BE:ED=1:1.
Приложения:
Ответил n06050802rfnz
0
Спасибо, конечно, но в ответах ОГЭ там 1:1
Ответил nafanya2014
0
Да, ошиблась в расчетах и АВ=2 взяла, а надо 3
Ответил n06050802rfnz
0
Все, все идеально
Новые вопросы
Математика,
2 года назад
Другие предметы,
2 года назад
Литература,
8 лет назад
Математика,
8 лет назад
Литература,
9 лет назад