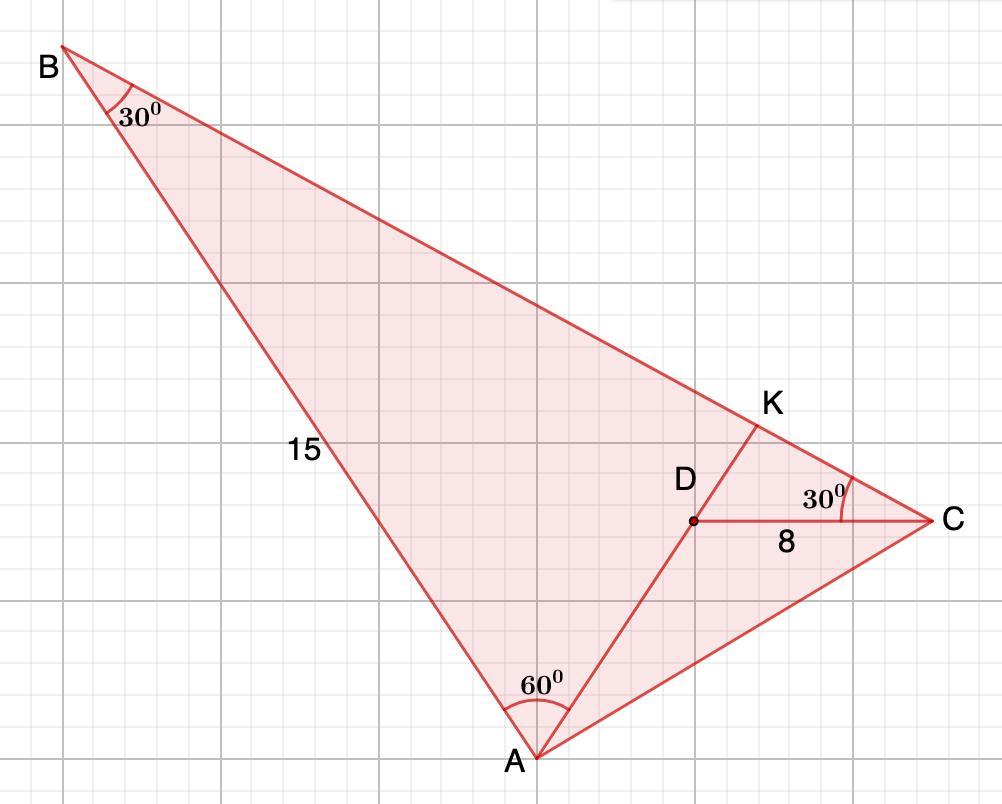
Внутри треугольника ABC выбрана точка D так, что ∠BAD=60∘ и ∠ABC=∠BCD=30∘. Известно, что AB=15 и CD=8. Найдите длину отрезка AD. Если необходимо, округлите ответ до 0.01 или запишите его в виде обыкновенной дроби.

Ответ:

AD=3,5 (ед)

Объяснение:

Дано: ΔАВС;

∠BAD=60°; ∠ABC=∠BCD=30°;

AB=15; CD=8.

Найти: АD

Решение:

1. Рассмотрим ΔАВК.

∠BAD=60°; ∠ABС=30°

Сумма углов треугольника равна 180°.

⇒∠АКВ=180°-(∠BAD + ∠ABС)=180°-(60°+30°)=90°

⇒ ΔАВК - прямоугольный.

Катет, лежащий против угла 30°, равен половине гипотенузы.

⇒ АК=АВ:2 = 15:2=7,5

2. Рассмотрим ΔDKC - прямоугольный. (п.1)

∠КСD=30° (условие)

⇒ DK=DC:2=8:2=4

3. AD=AK-DK=7,5-4=3,5 (ед)