Внимание!!! Трудные задачи! Прошу помочь решить две задачки (есть ответ, но не понимаю, как решать):
1) Треугольник MKP - прямоугольный, ∡К= 90°. Точка А, лежащая вне плоскости треугольника равноудалена от сторон этого треугольника на 8 см. Найдите расстояние от точки А до плоскости MKP, если MP= 13 см, KP= 12 см. {Ответ: 2√15}
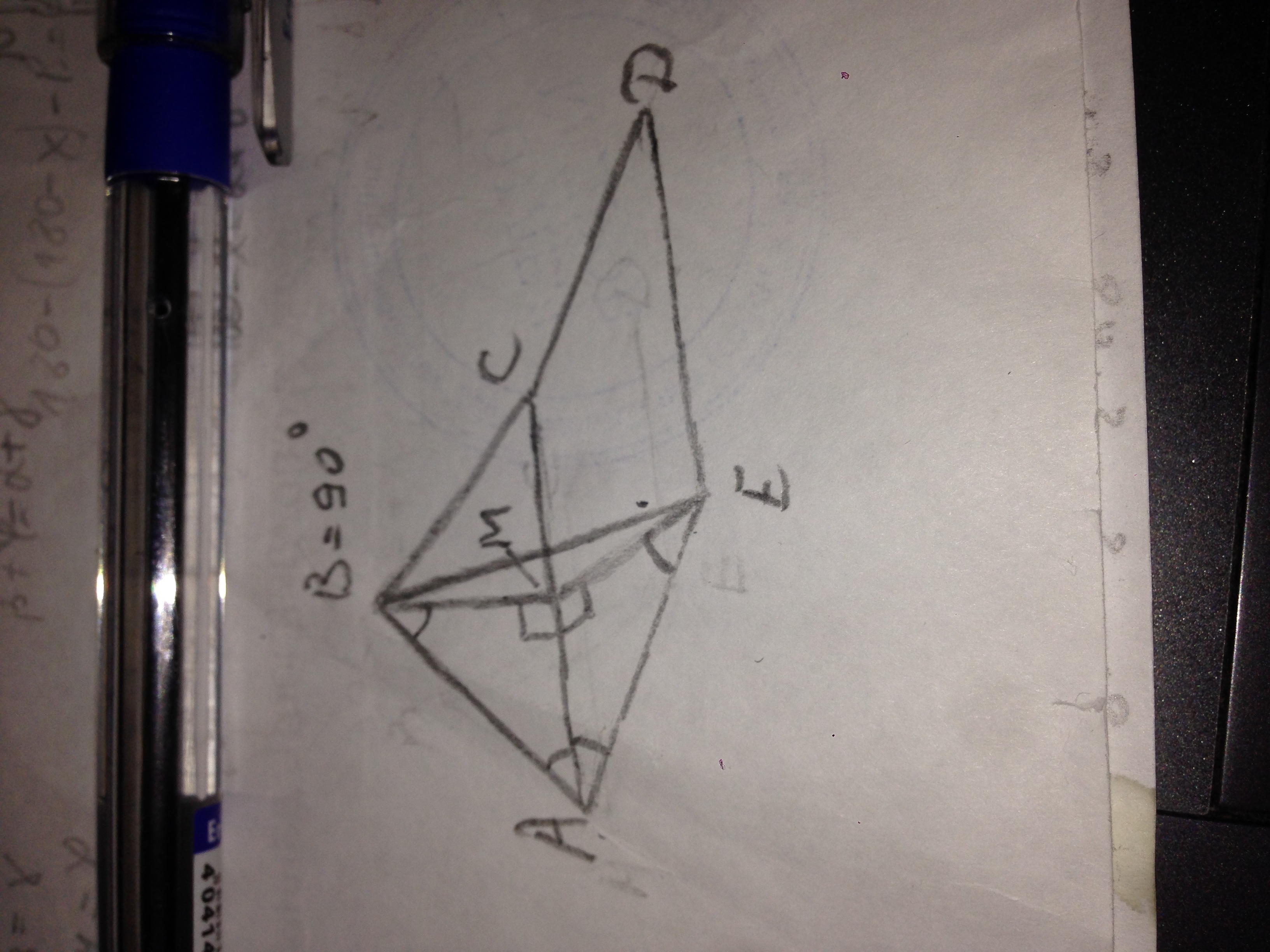
2) Треугольник ABC — равнобедренный, ∡ABC= 90°, ACDE — ромб, ∡CAE= 45°. Найдите косинус угла между плоскостями треугольника и ромба, если расстояние от точки B до прямой DE равно 4√5 см и AB= 8 см. {Ответ: 1/(4√2)}
Ответы на вопрос
Ответил ssoxo
0
2) Т.к. АВС - равнобедренный тр-ник, то высота, опущенная на основание является биссектрисой и высотой. Опустим высоту ВМ, ∠А=∠С=45°. Т.к. ∠АВМ=45° , то ВМ=АМ. ВМ=АВ·sin45=8√2/2=4√2 см.
В прямоугольном тр-ке АМЕ ∠МАЕ=∠МЕА=45°, значит АМ=МЕ ⇒ ВМ=МЕ.
В тр-ке ВМЕ ВЕ=4√5 см (по условию).
По теореме косинусов:
cosМ=(ВМ²+МЕ²-ВЕ²)/(2·ВМ·МЕ)=(32+32-(4√5)²)/(2·4√2·4√2)=-1/4 - вот это ответ.
В прямоугольном тр-ке АМЕ ∠МАЕ=∠МЕА=45°, значит АМ=МЕ ⇒ ВМ=МЕ.
В тр-ке ВМЕ ВЕ=4√5 см (по условию).
По теореме косинусов:
cosМ=(ВМ²+МЕ²-ВЕ²)/(2·ВМ·МЕ)=(32+32-(4√5)²)/(2·4√2·4√2)=-1/4 - вот это ответ.
Приложения:
Ответил ВладEagle
0
Ответ: 1/4√2
Ответил ssoxo
0
может в условии что напутано, ход решения верный.
Ответил ВладEagle
0
По аналогии с предыдущим решением я пришел в этой задаче к правильному ответу.
Ответил ssoxo
0
В том и фокус, что точка Е не равноудалена от вершин тр-ка АВС и ЕМ - это не перпендикуляр к плоскости АВС.
Новые вопросы