визначте похідну f(x)=6x^4+2x+3​

Ответ:

берем производную:

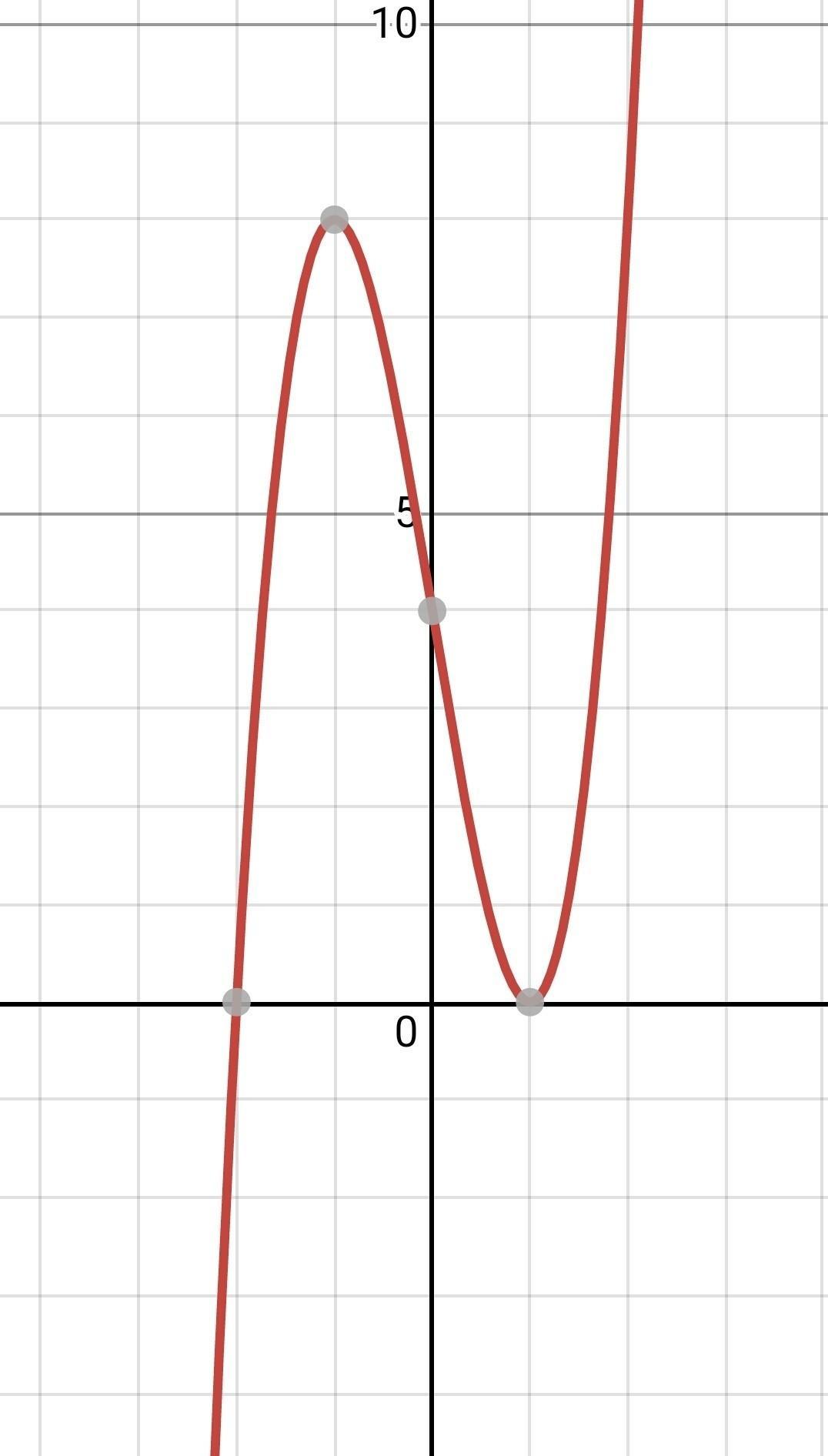
f(x)'=2(3x^2)-6=6x^2-6

ищем экстремиумы:

6x^2-6=0; x^2=1; x1=1; x2=-1

y1=0, y2=8;

у функции 2 экстремиума: (1;0) и (-1;8)

определяем методом интервалов возрастание/убывание:

возрастает: x=(-беск;-1] и [1;+беск)

убывает: x= [-1;1]

определаяем четность/нечетность:

f(-x)=2(-x)^3-6(-x)+4=-2x^3+6x+4=-(2x^3-6x-4) - функция не является ни четной ни нечетной;

ищем точки перегиба:

берем 2 производную:

f(x)''=6(2x)=12x

12x=0; x=0;

y=4; (0;4)

методом интервалов находим выпуклость/ вогнутсть:

выпукла: (-беск;0]

вогнута: [0;+беск)

собираем точки:

(1;0), (-1;8), (0,4)

и по ним строим график: